Screenshots
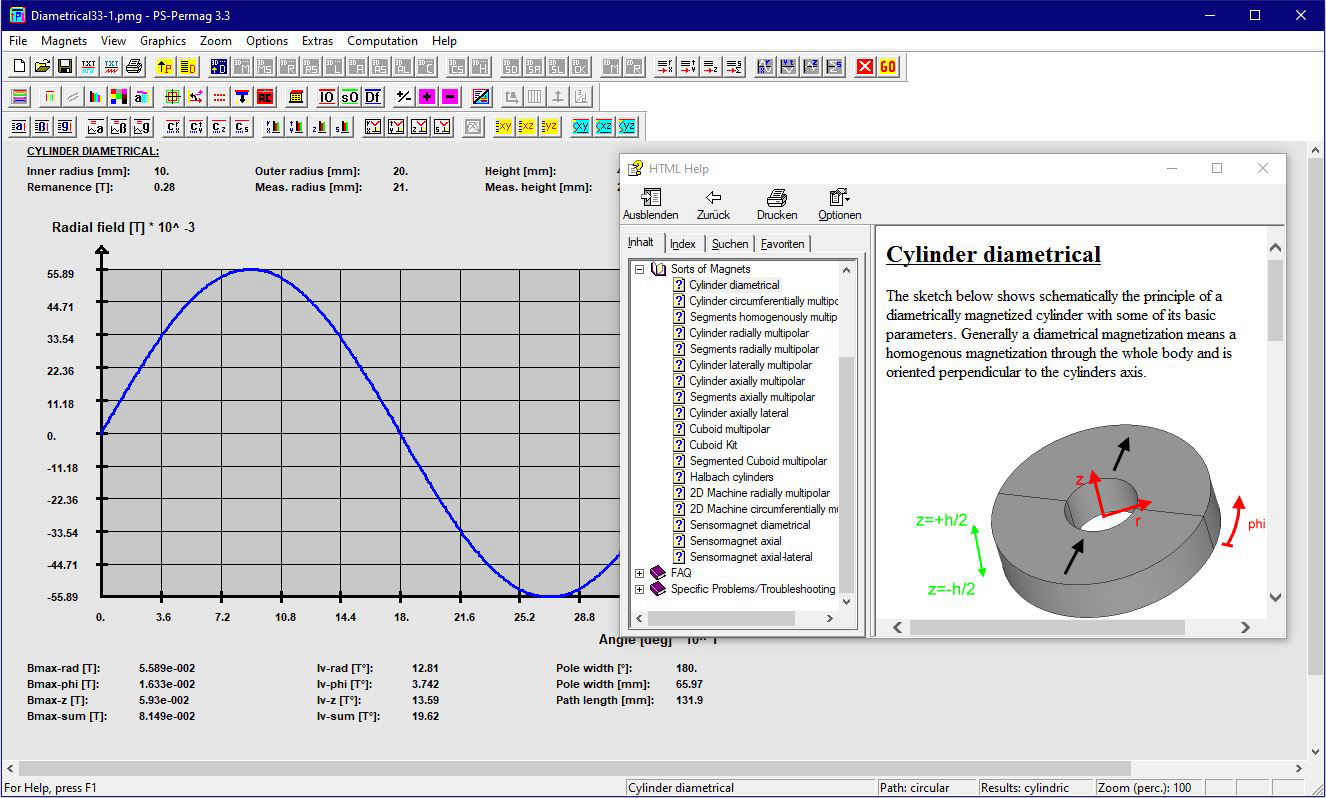
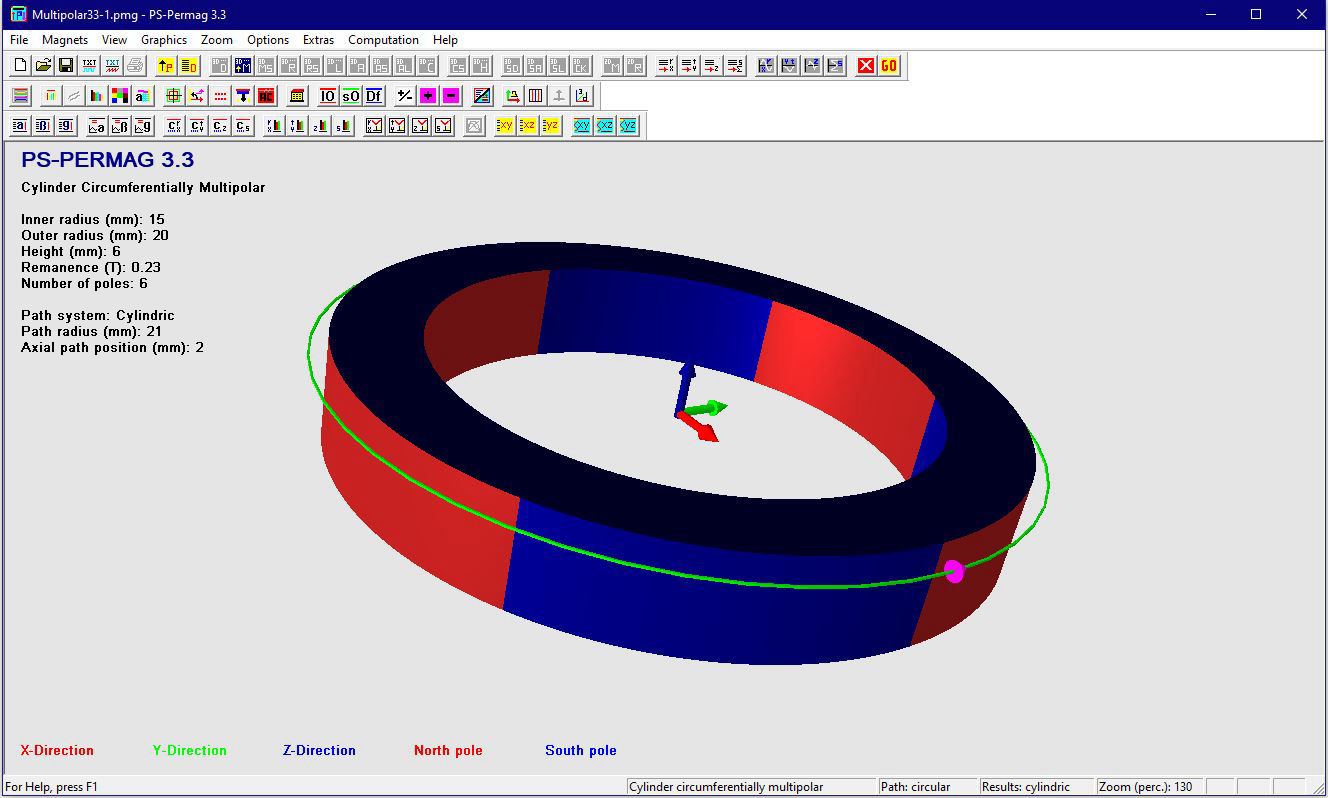
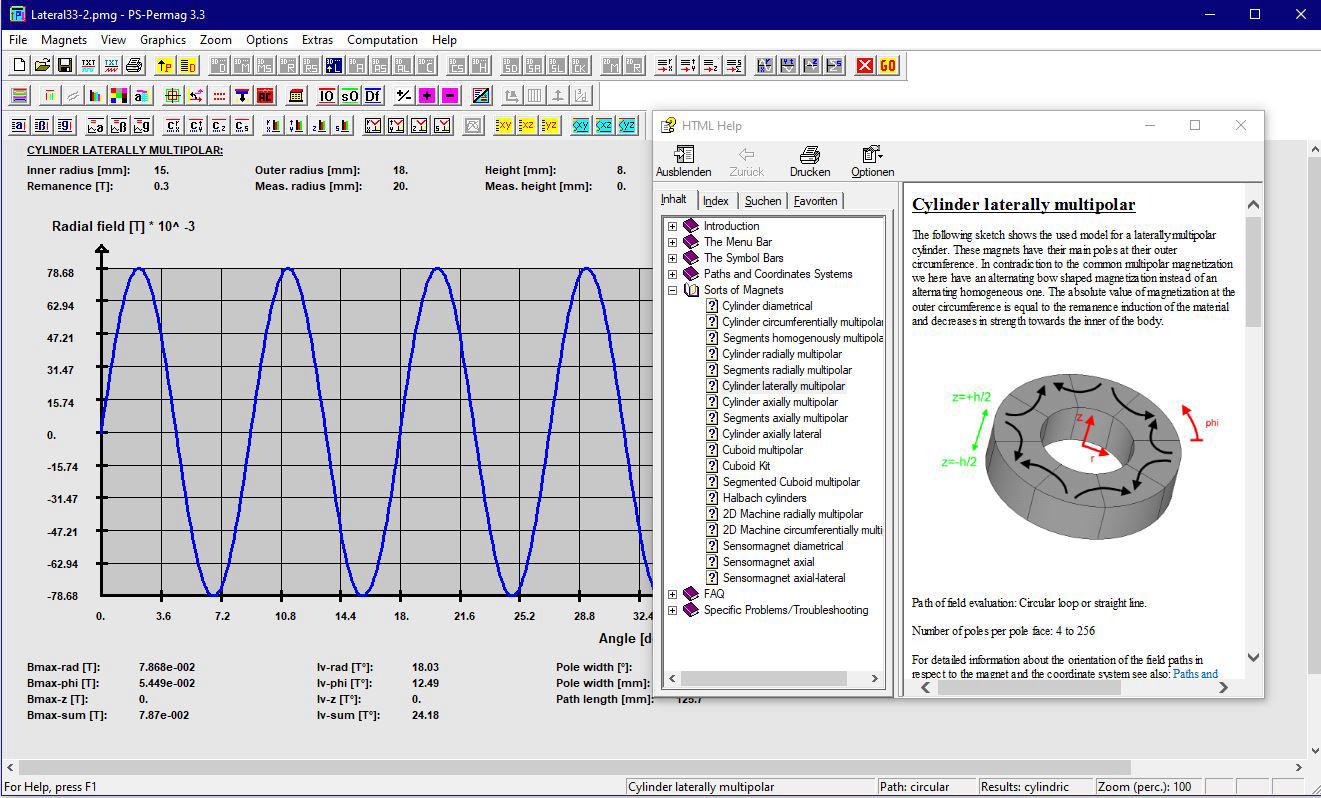
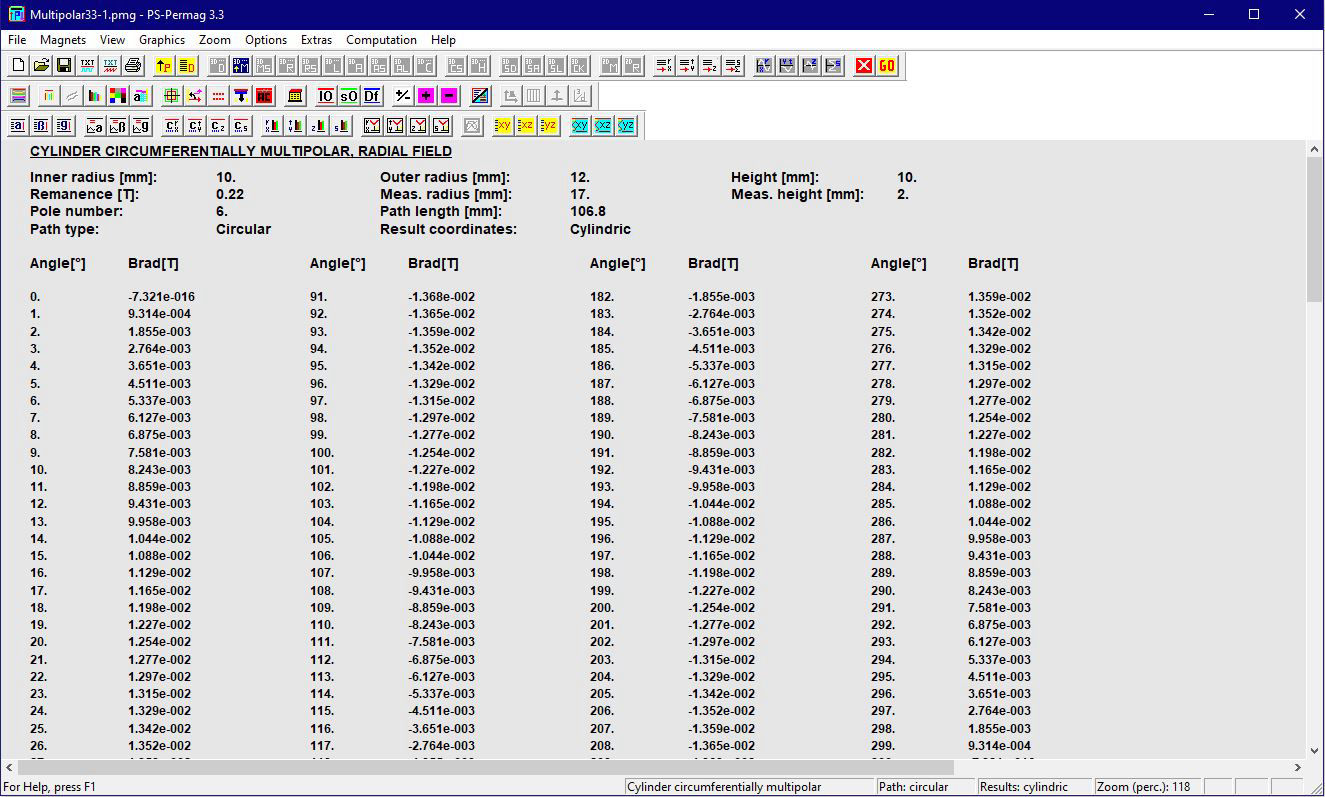
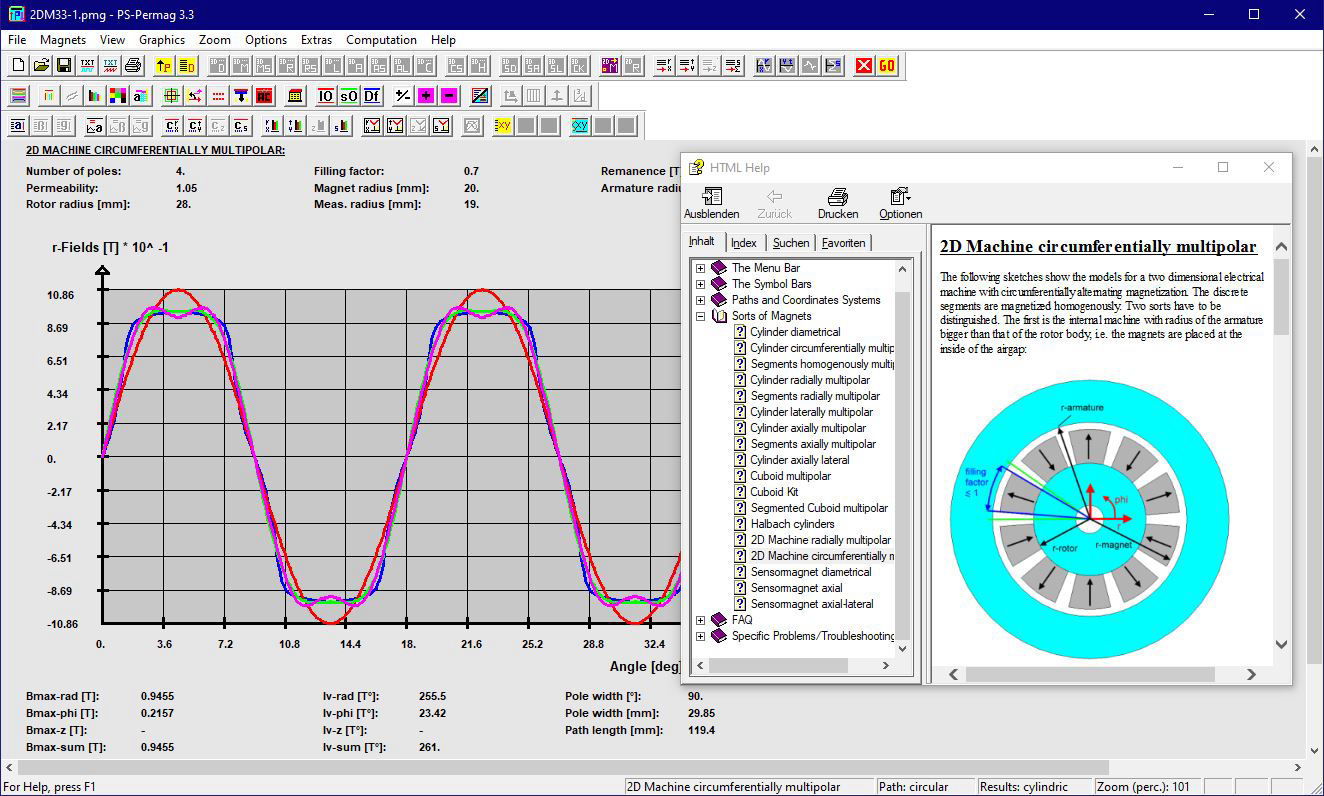
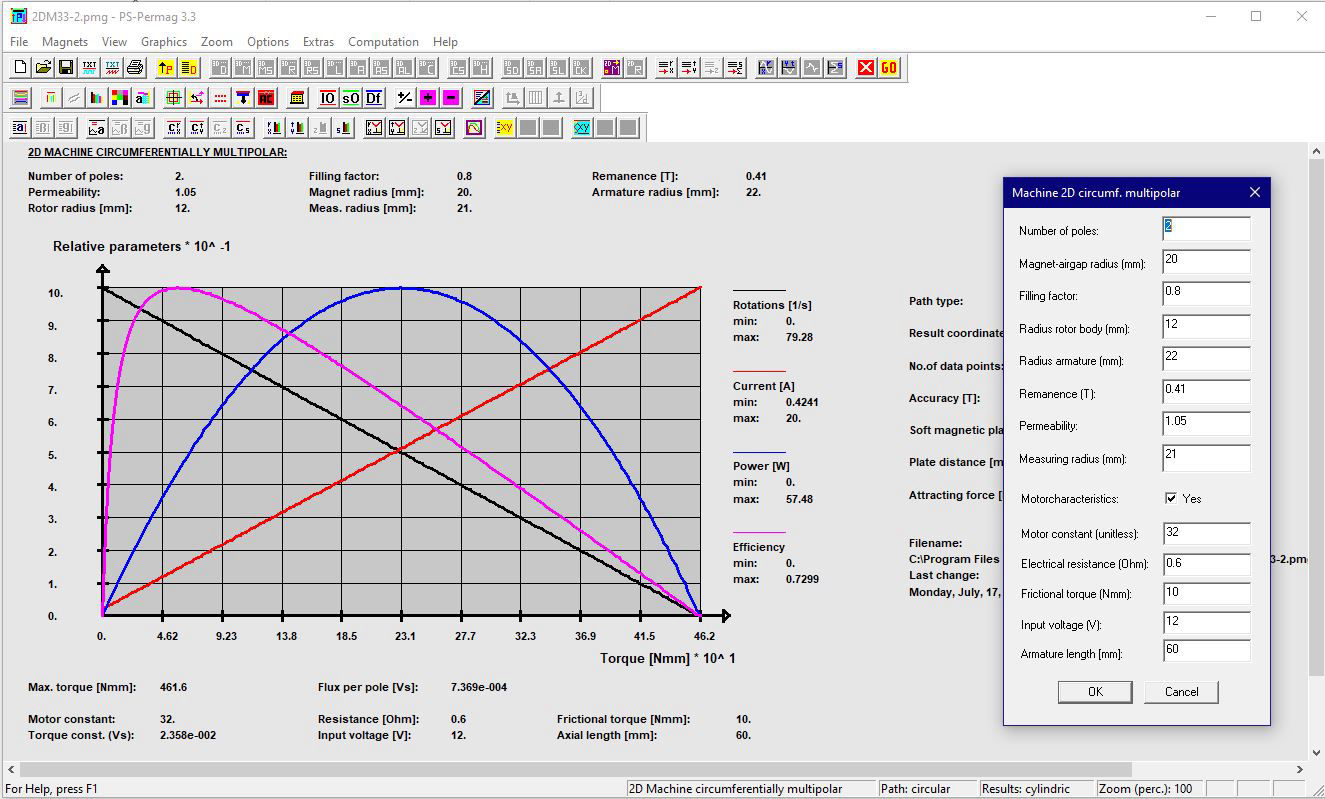
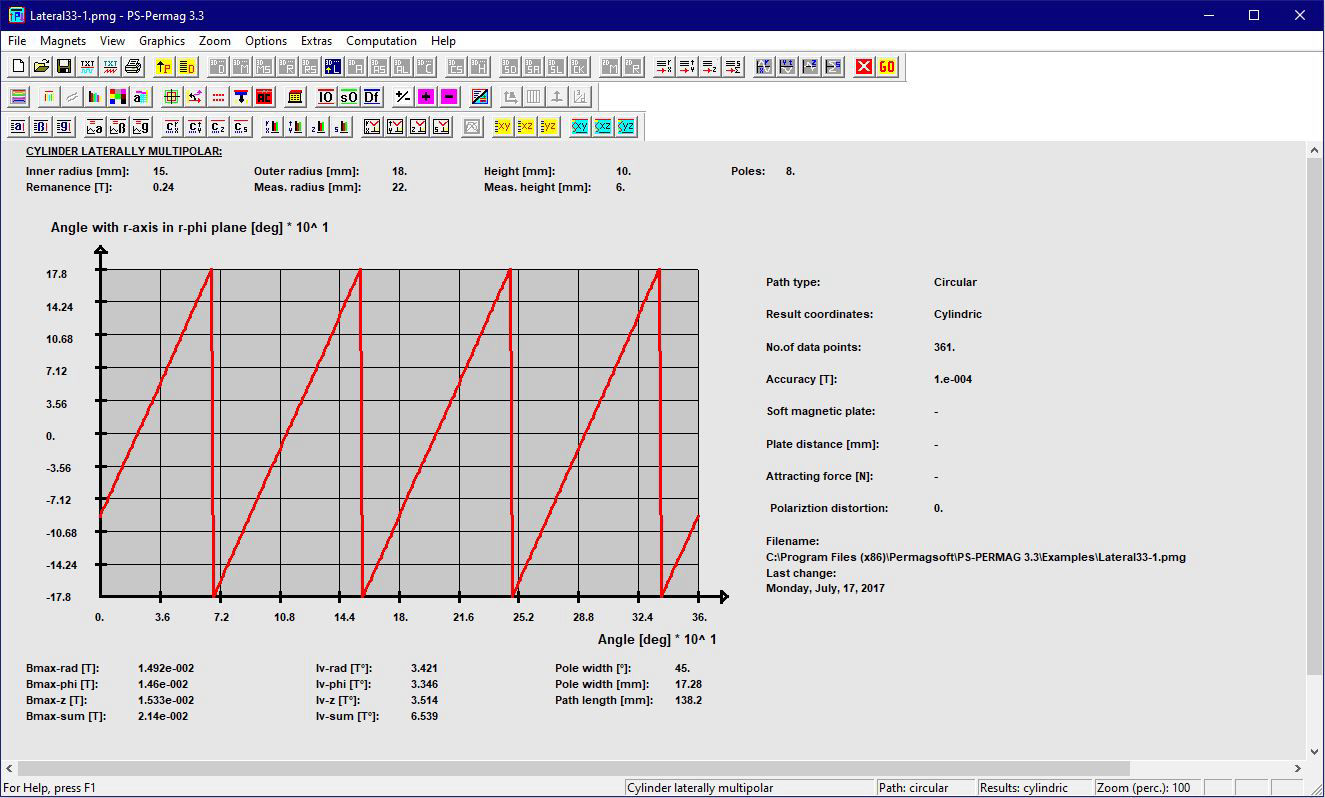
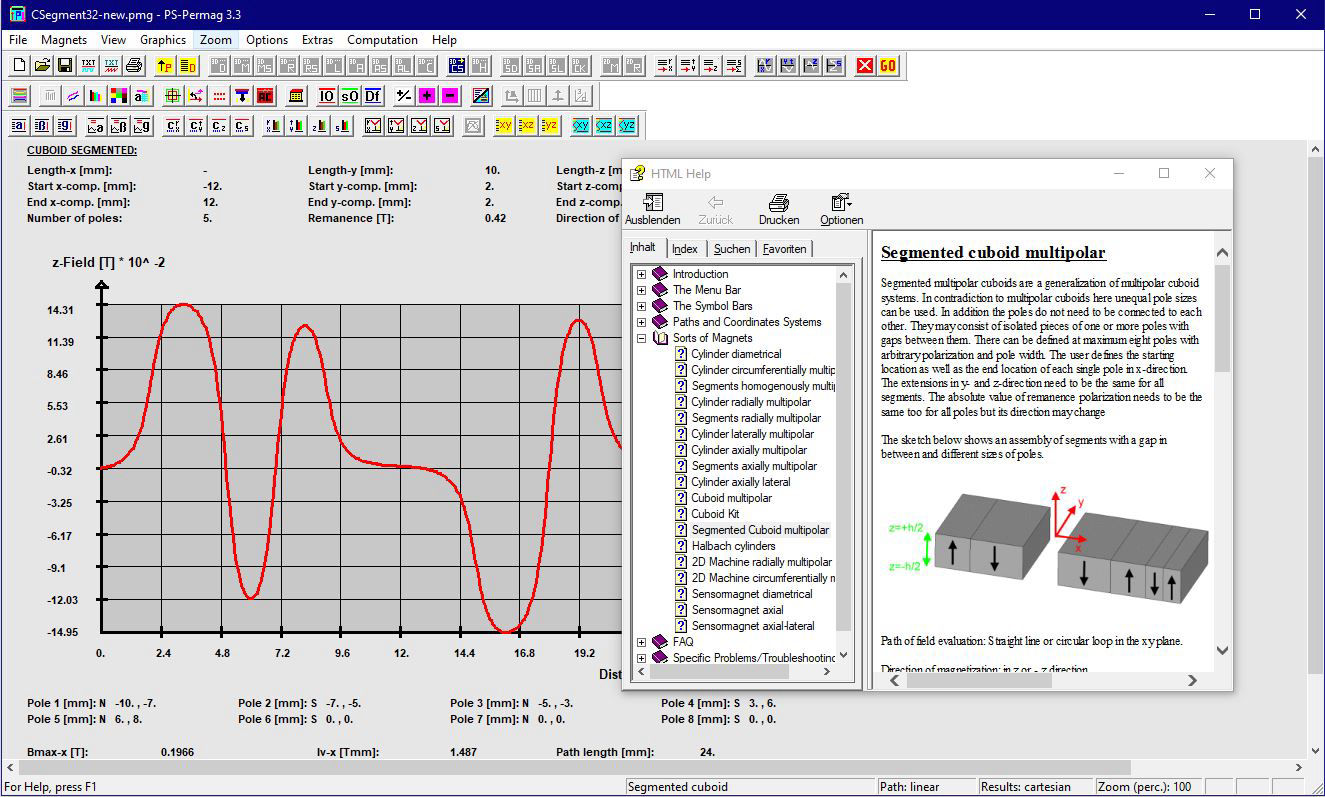
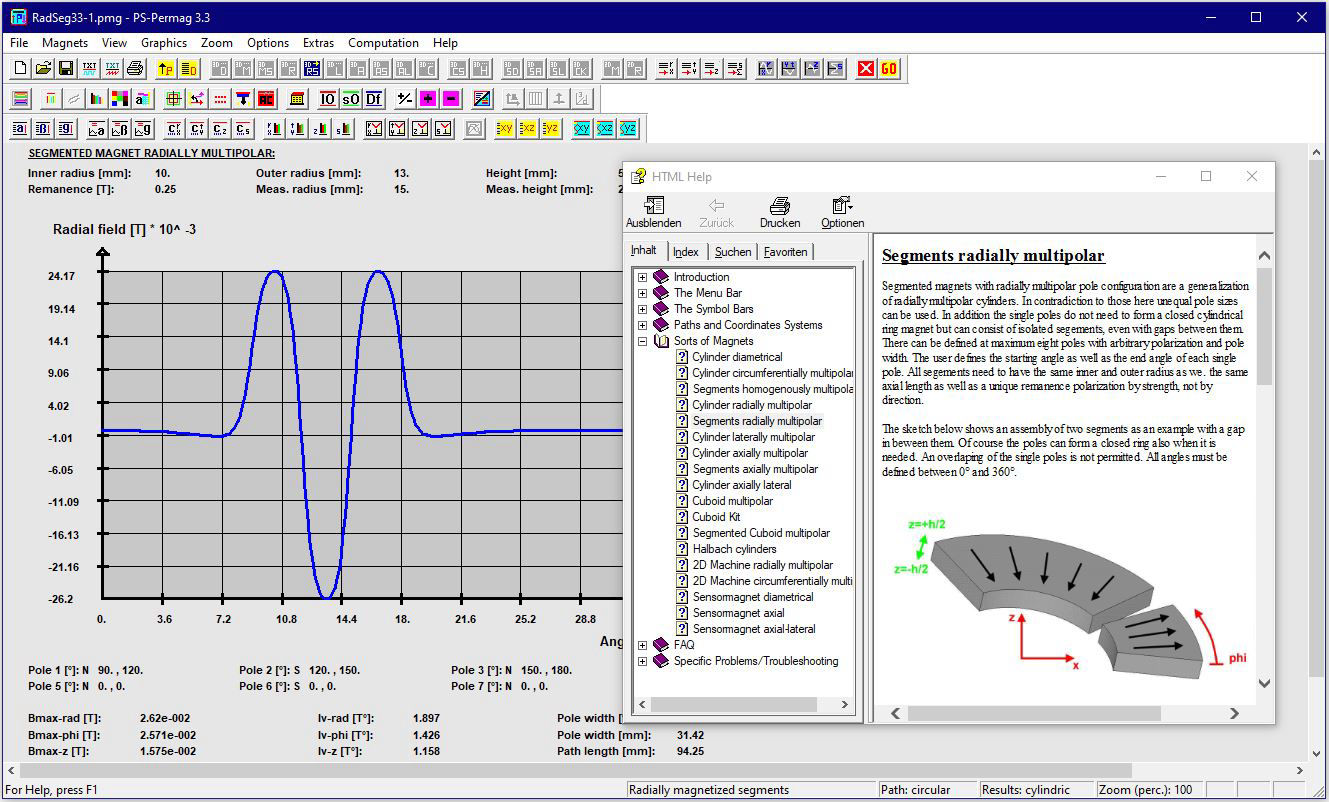
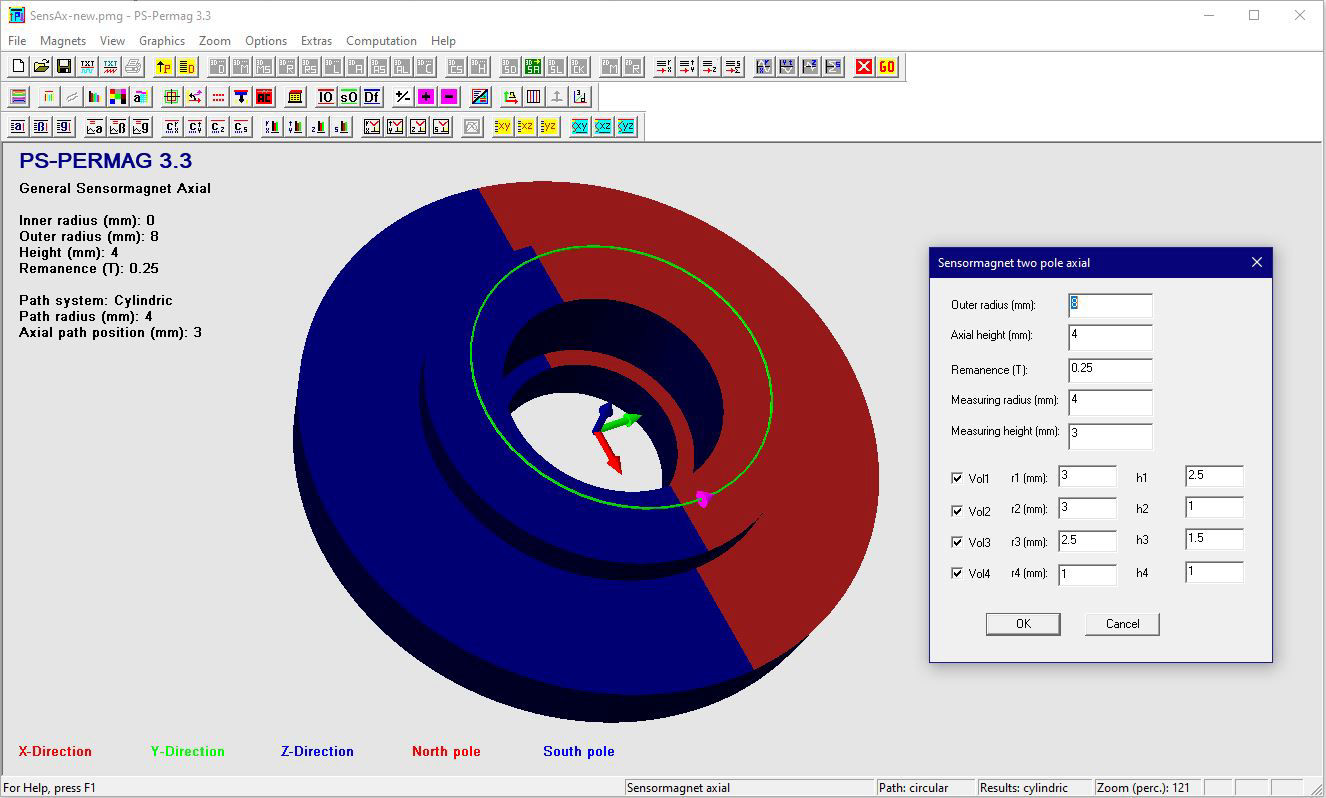
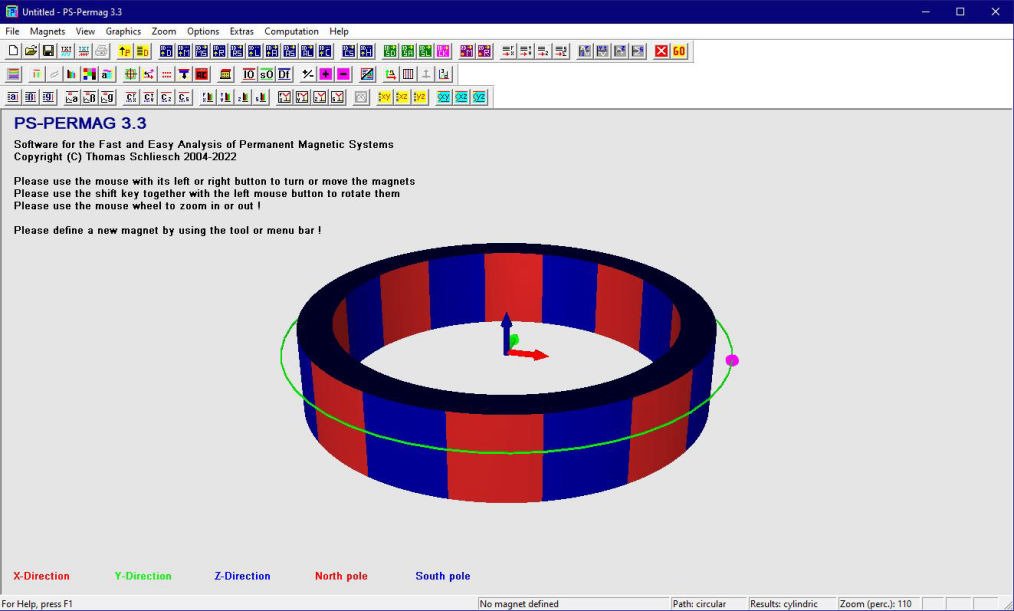
Schauen Sie sich ausgewählte Screenshots und zugehörige Texte an, um noch mehr über die Fähigkeiten von PS-PERMAG zu lernen

Schauen Sie sich ausgewählte Screenshots und zugehörige Texte an, um noch mehr über die Fähigkeiten von PS-PERMAG zu lernen