Tutorien

Multipolar homogen magnetisierter Magnet mit sechs Polen

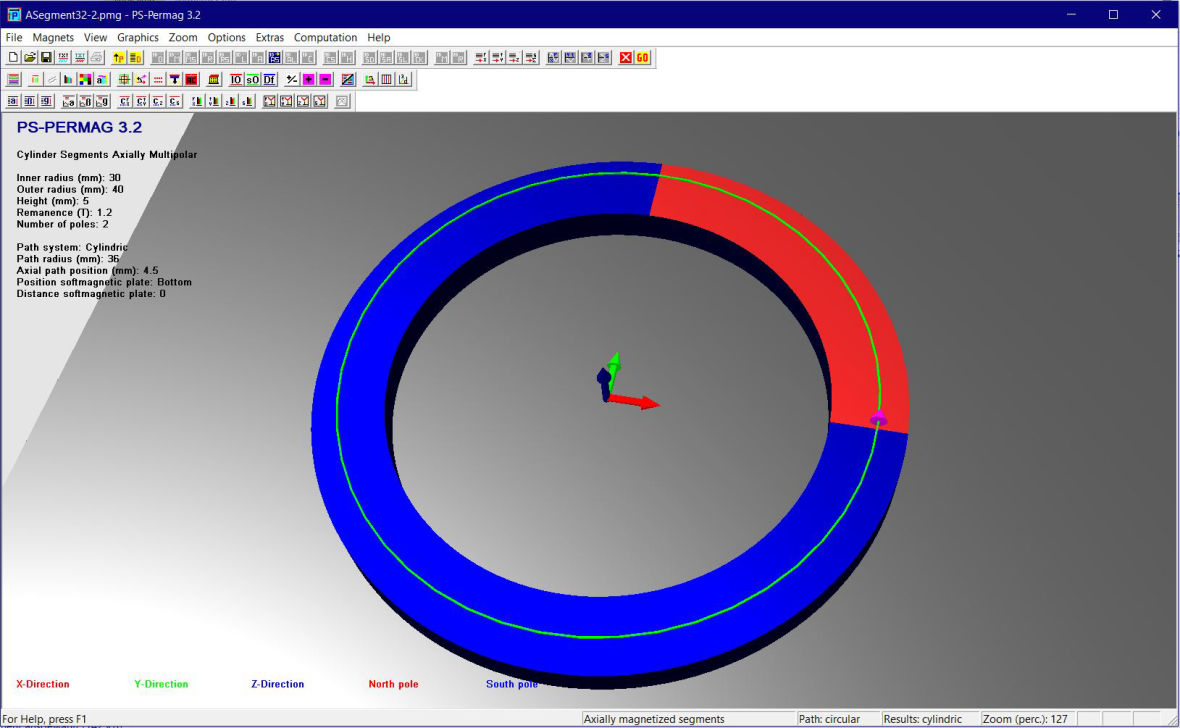
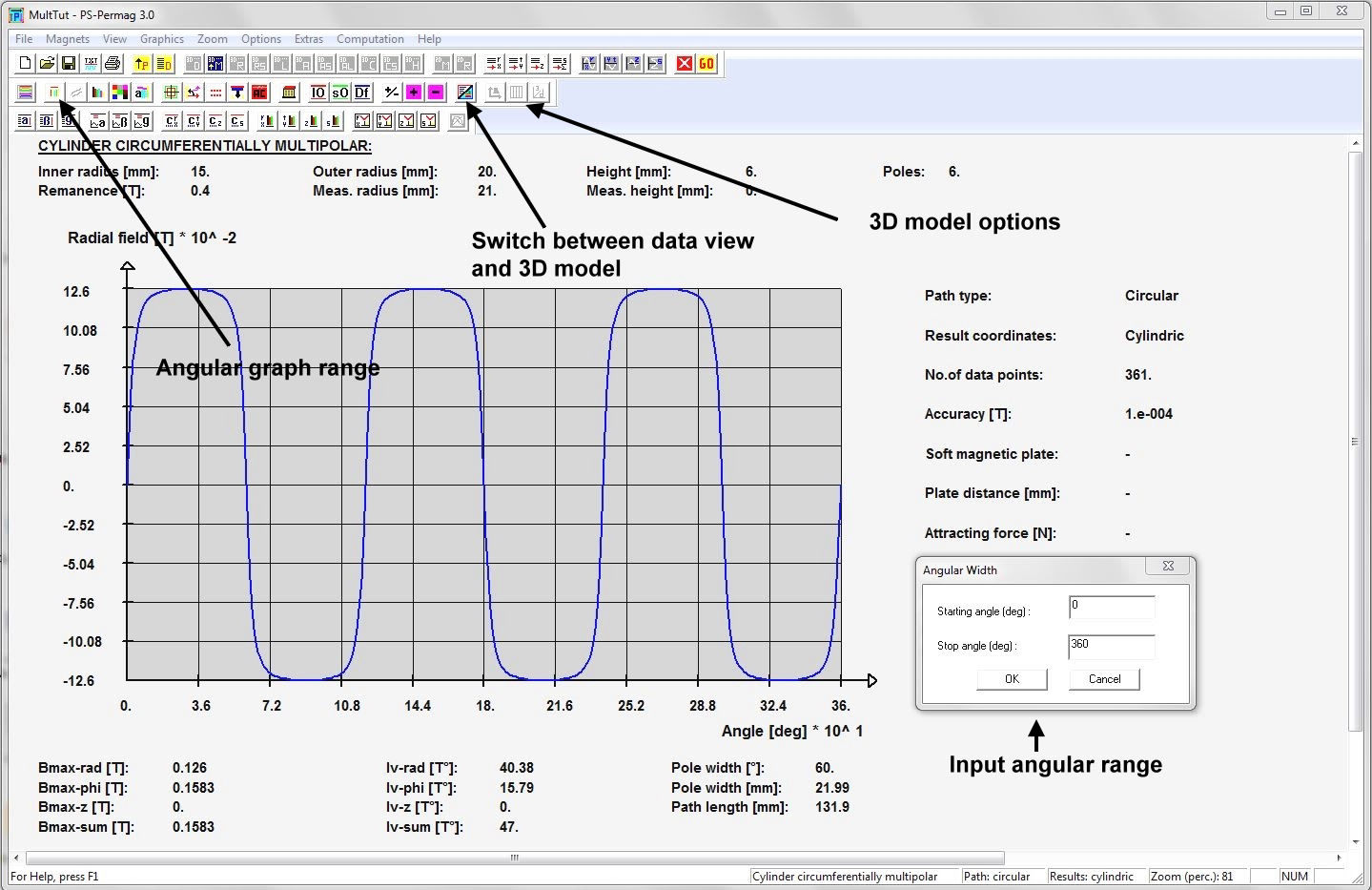
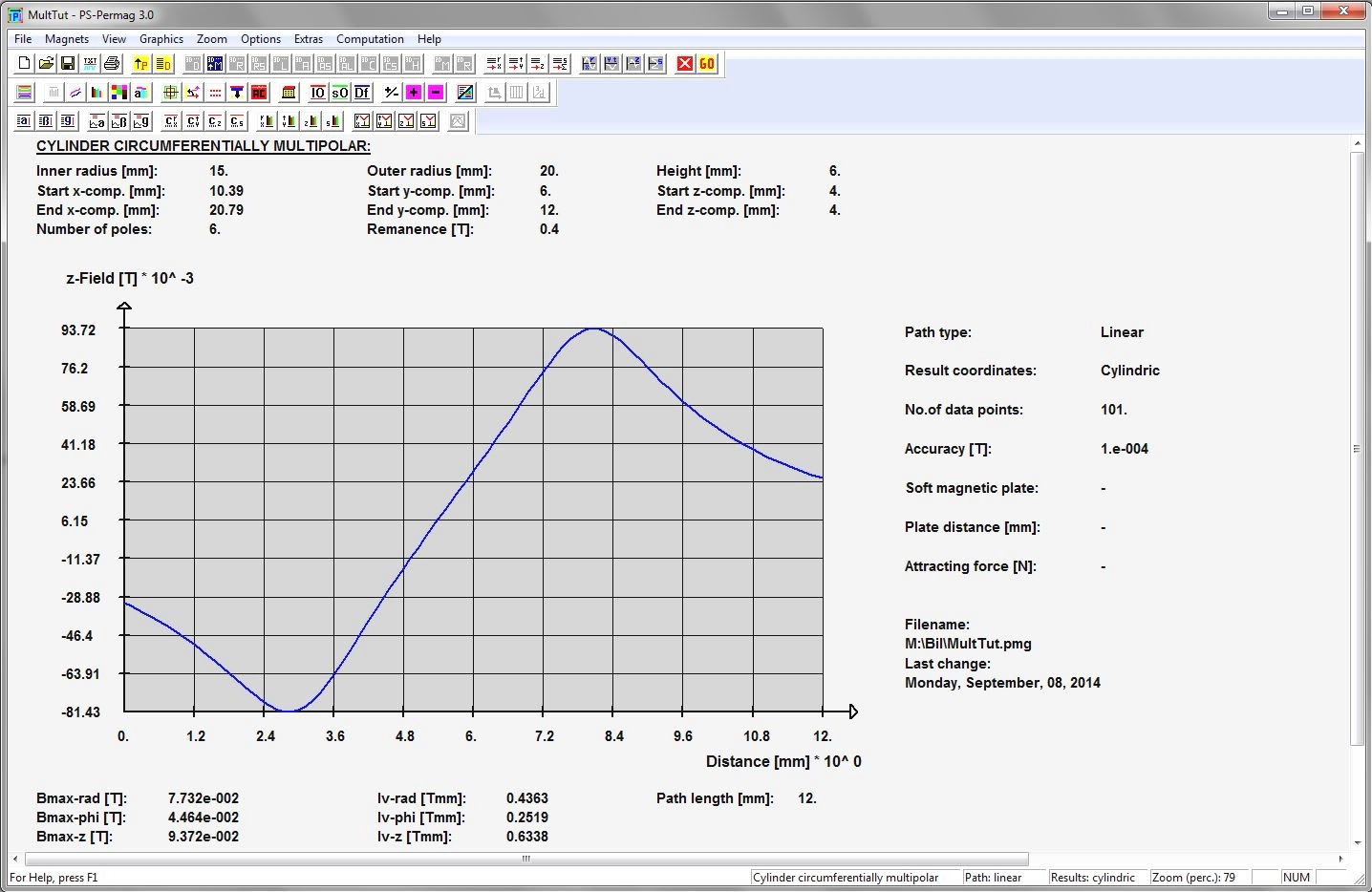
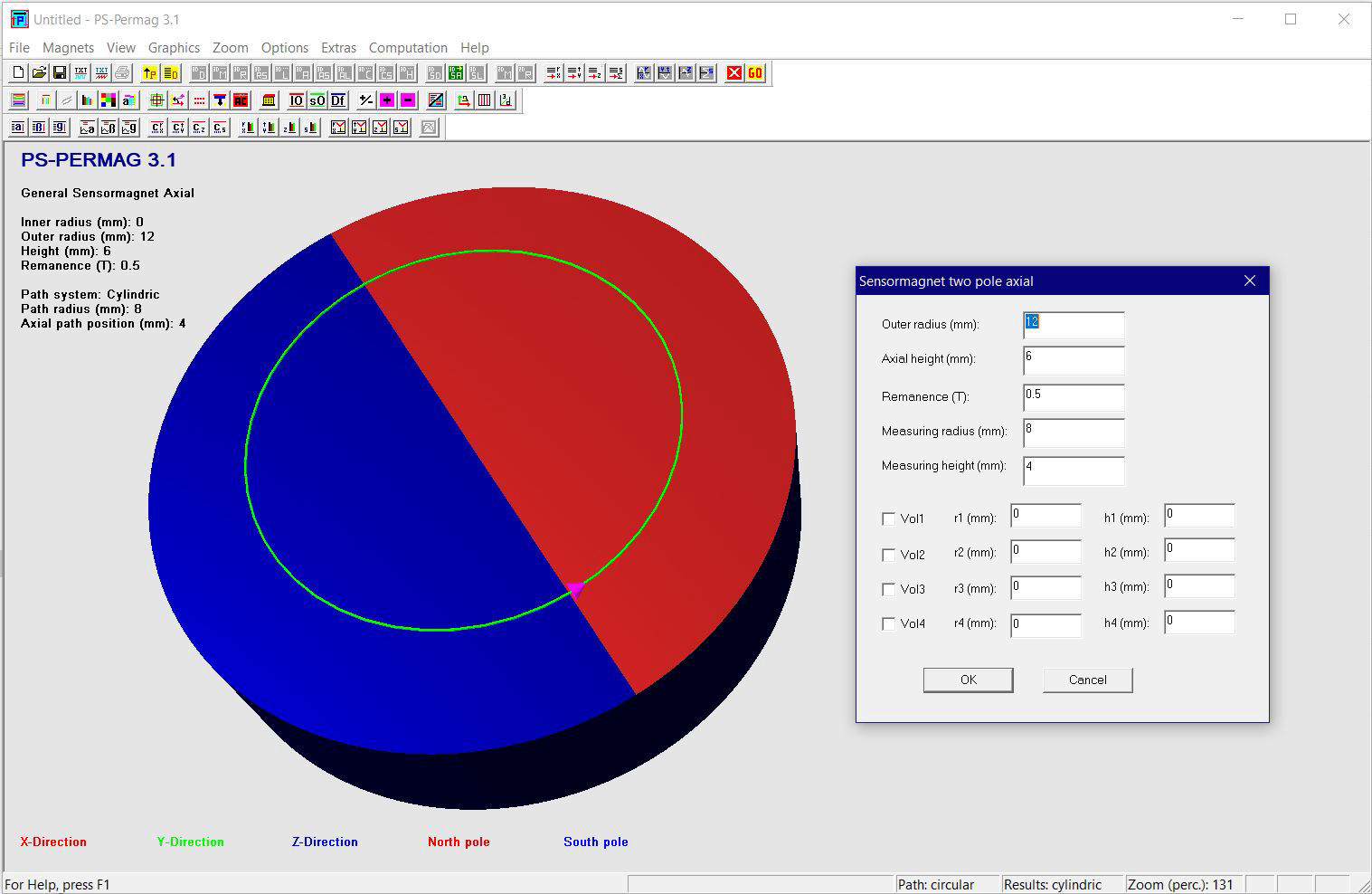
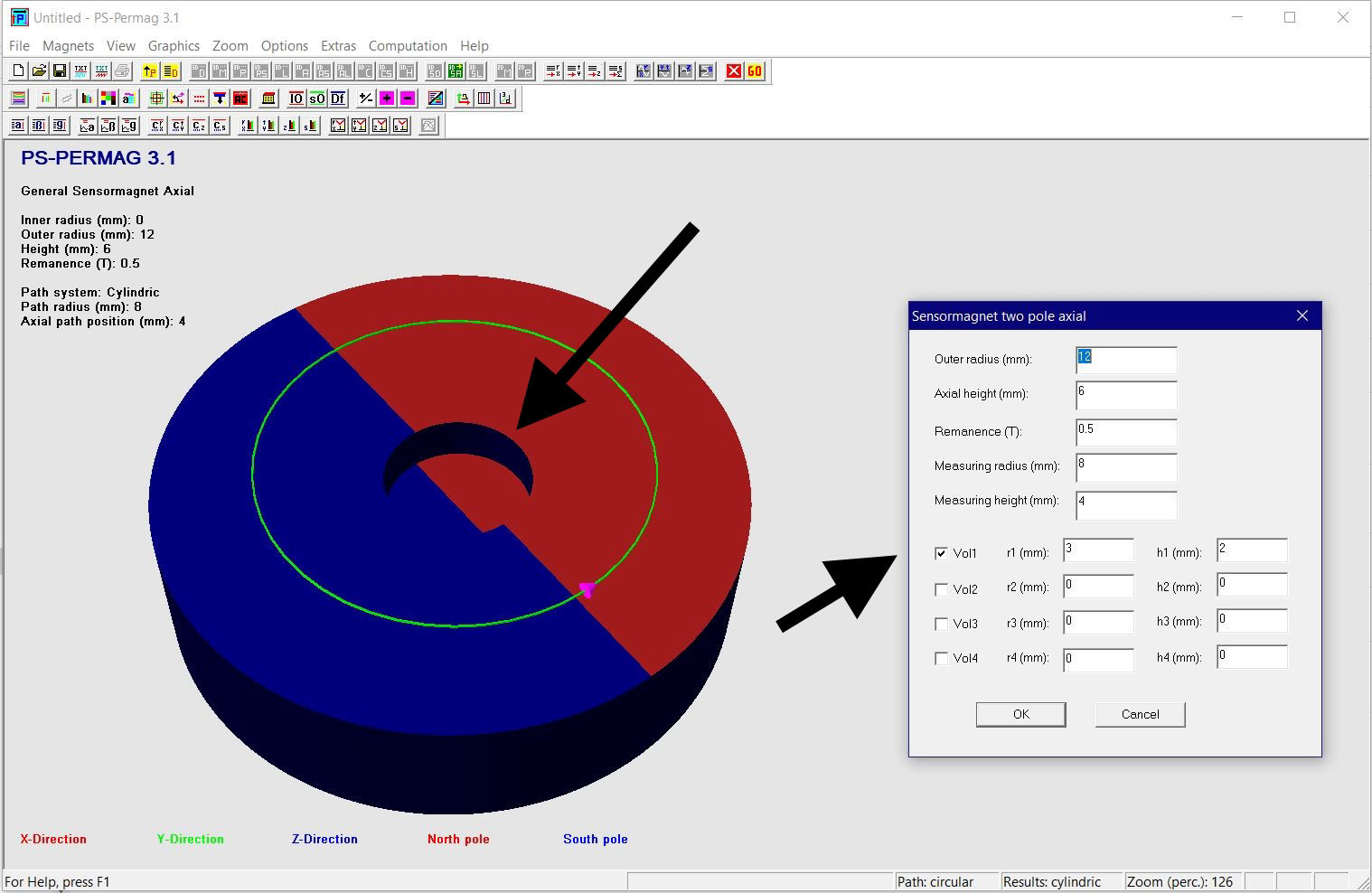
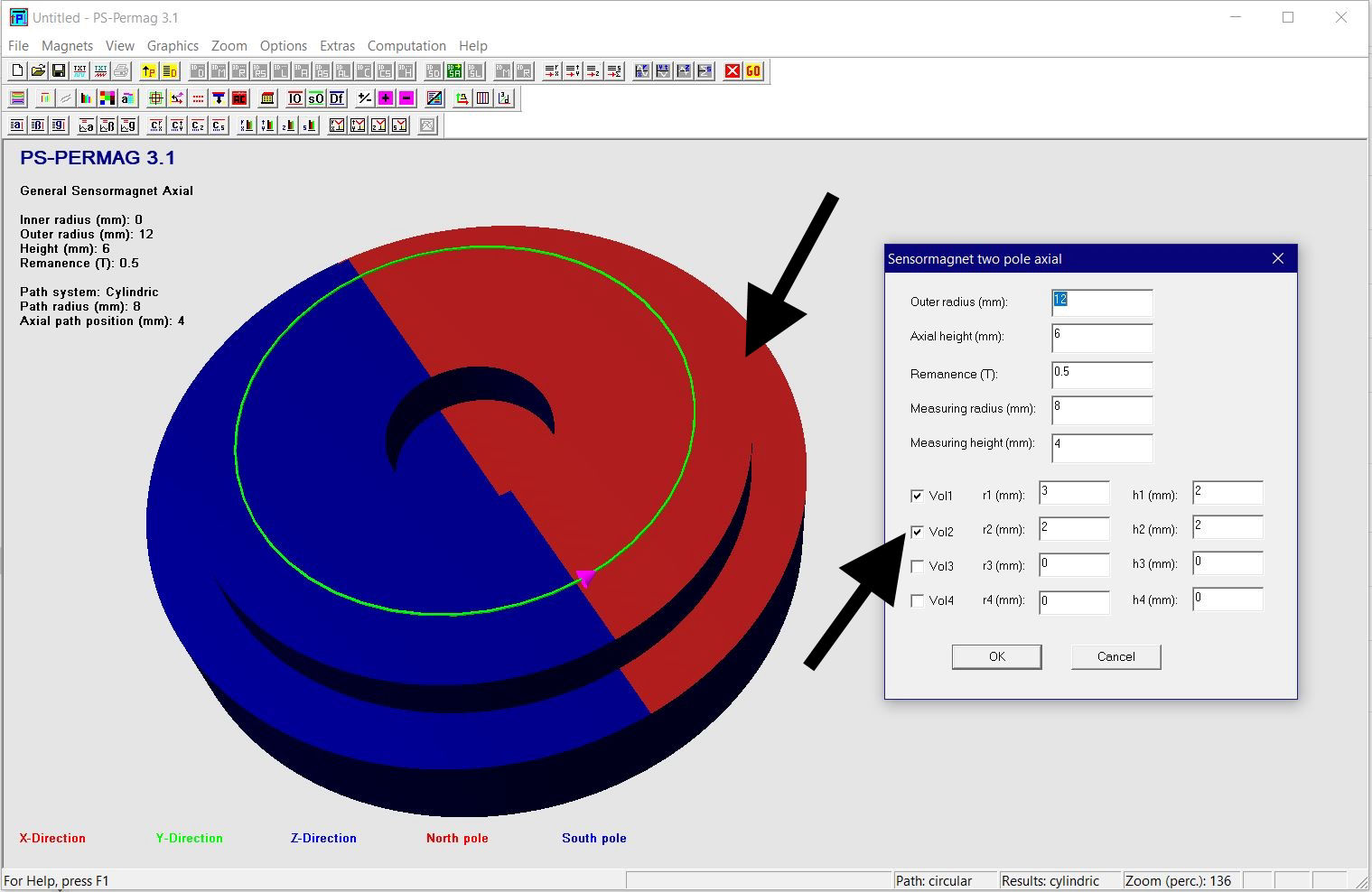
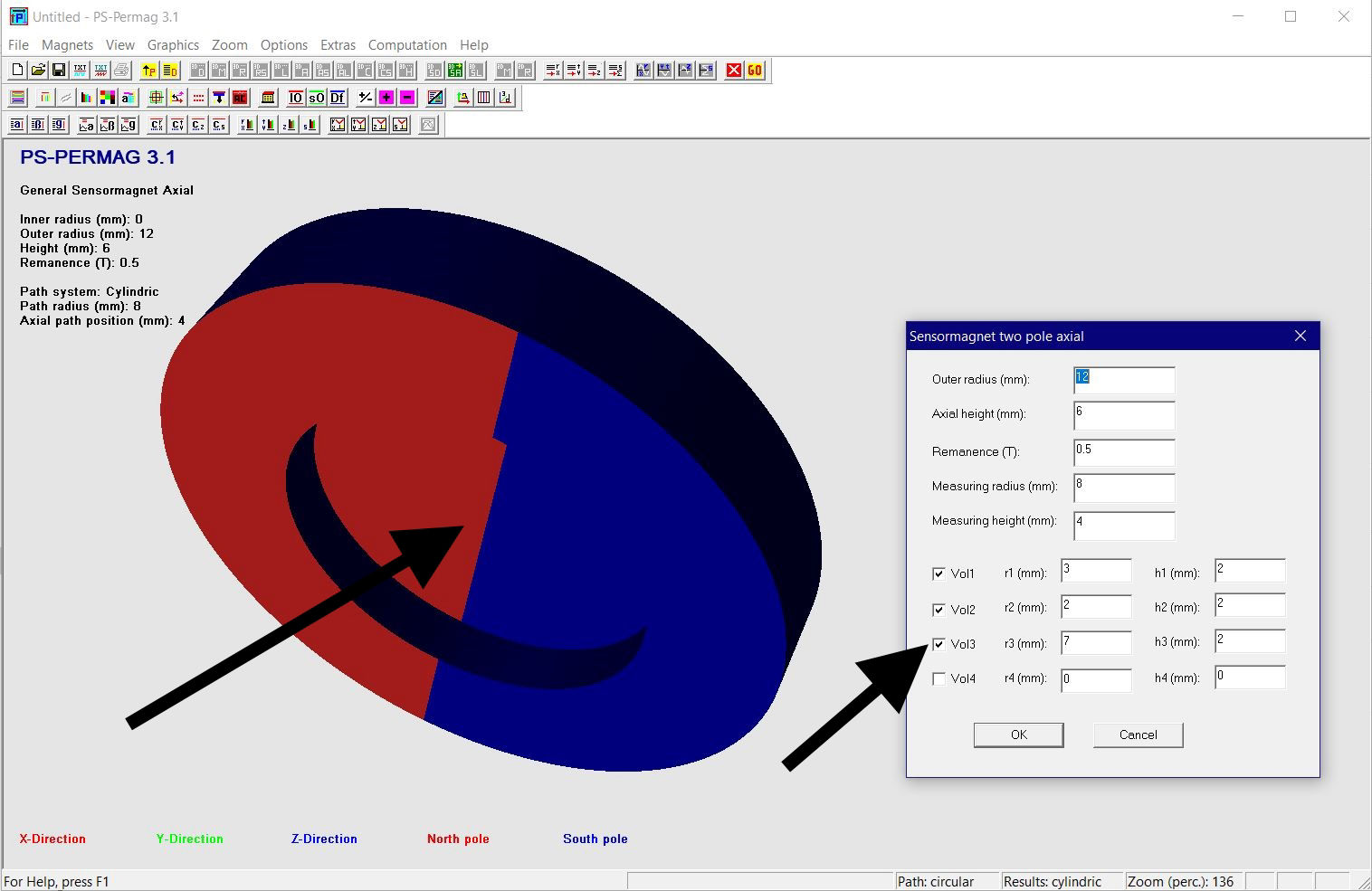
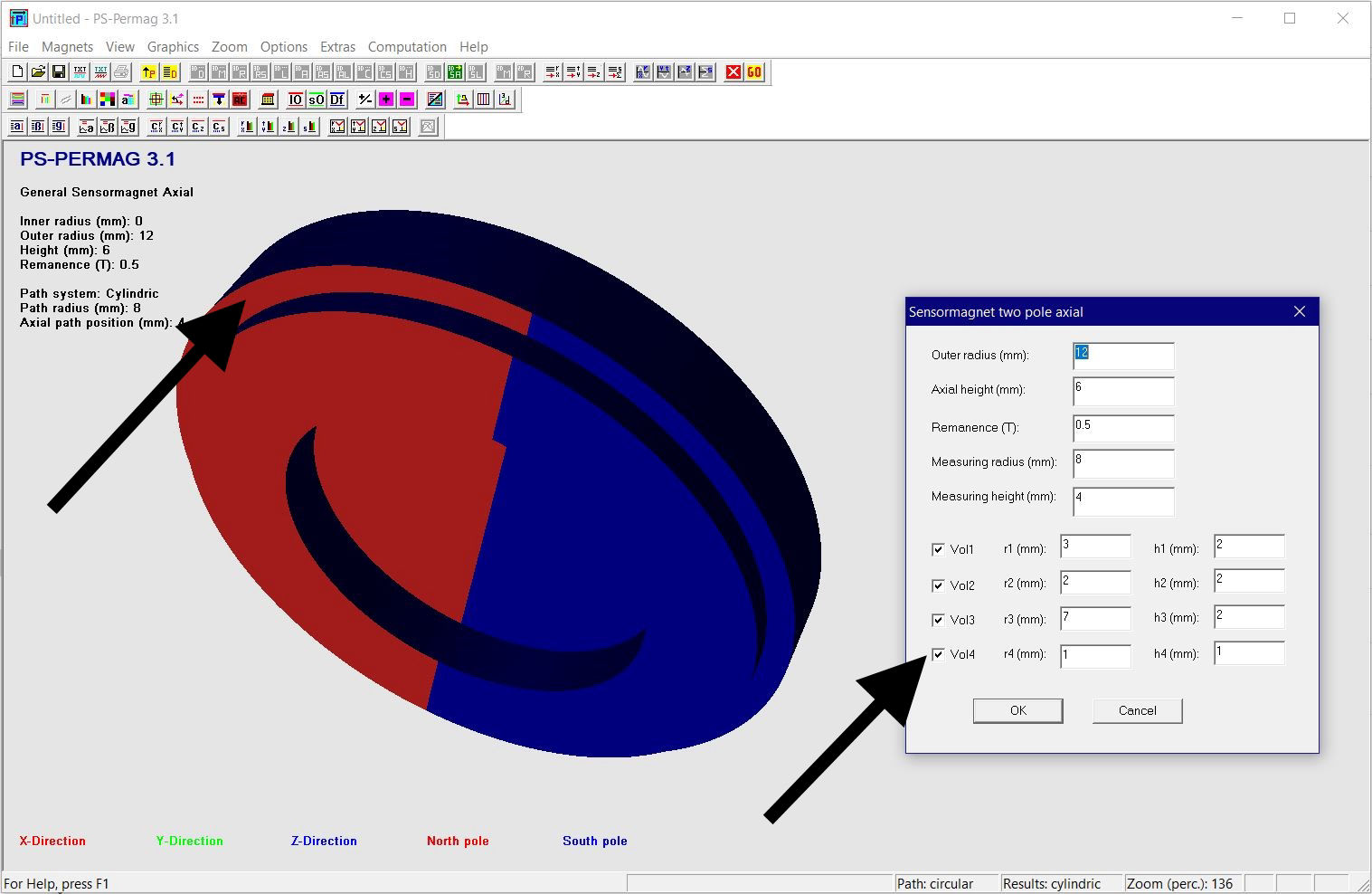
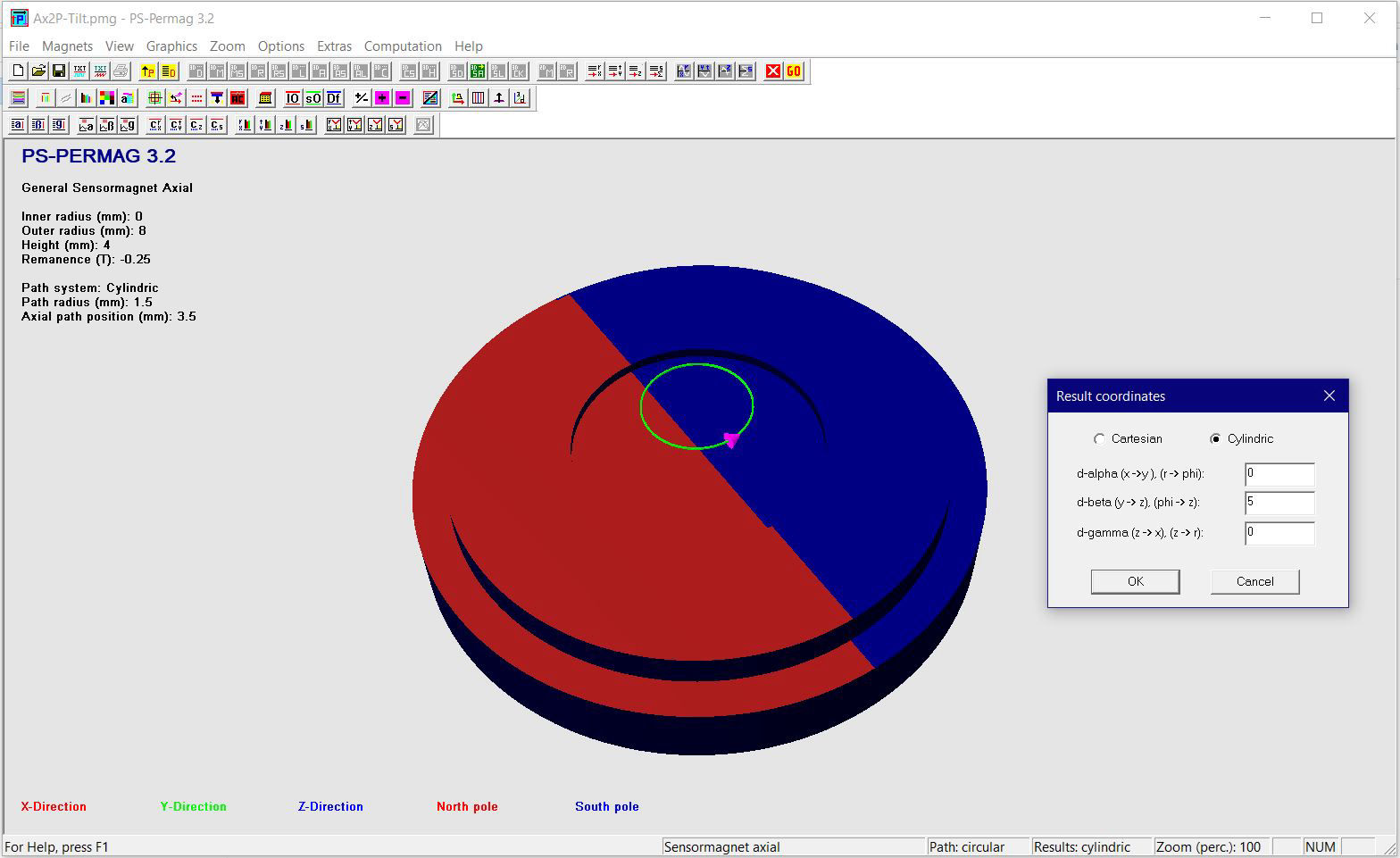
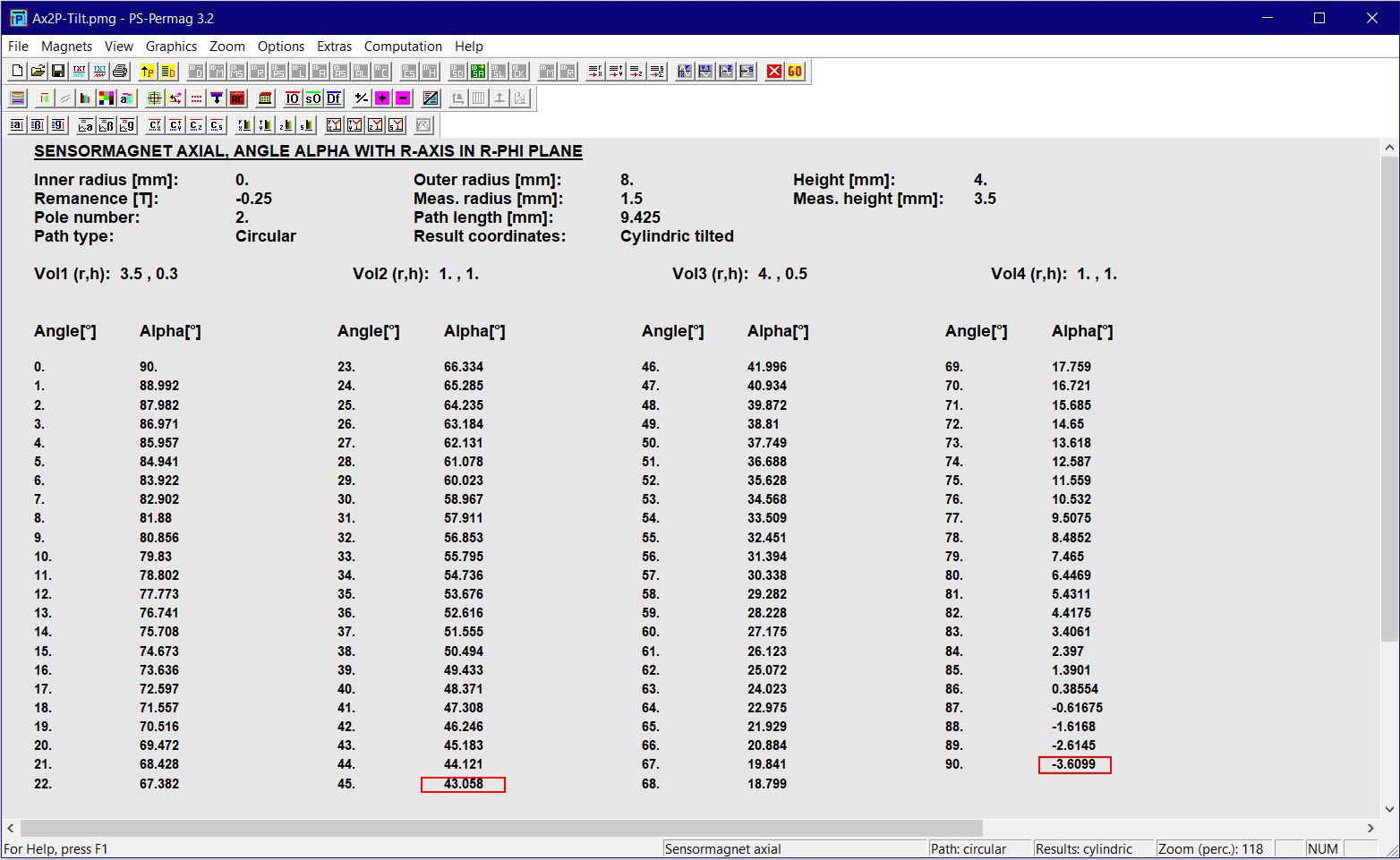
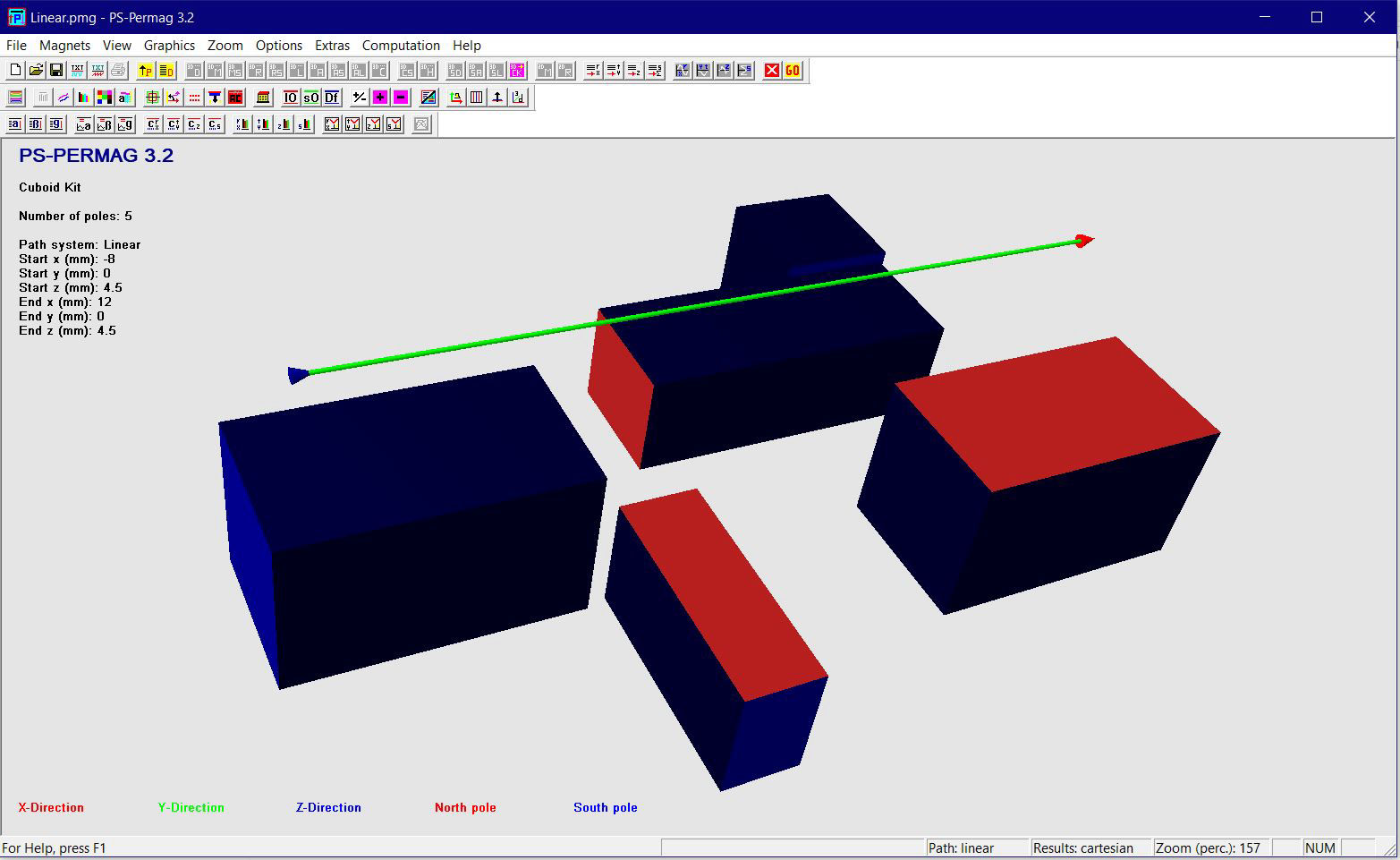
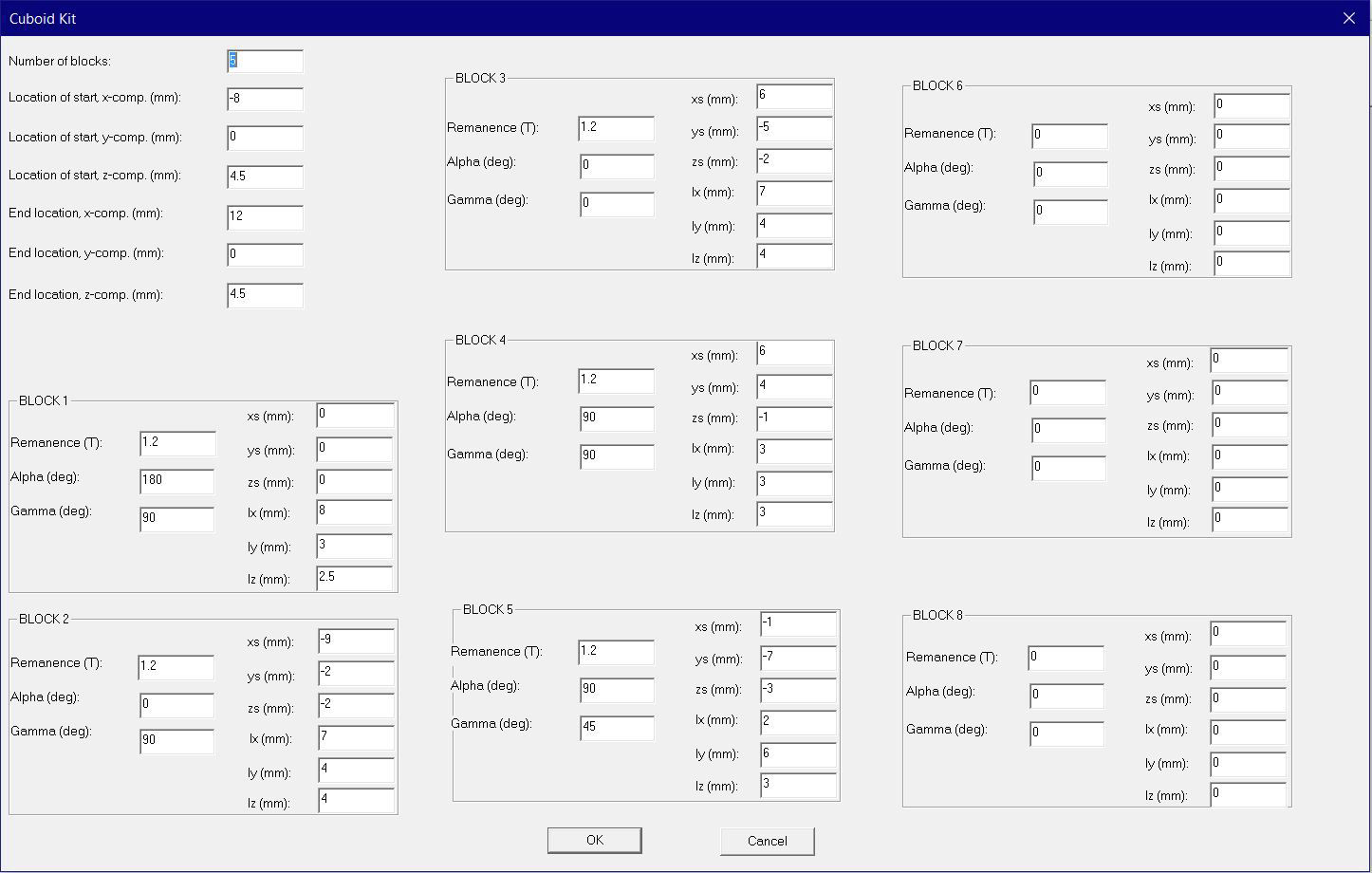
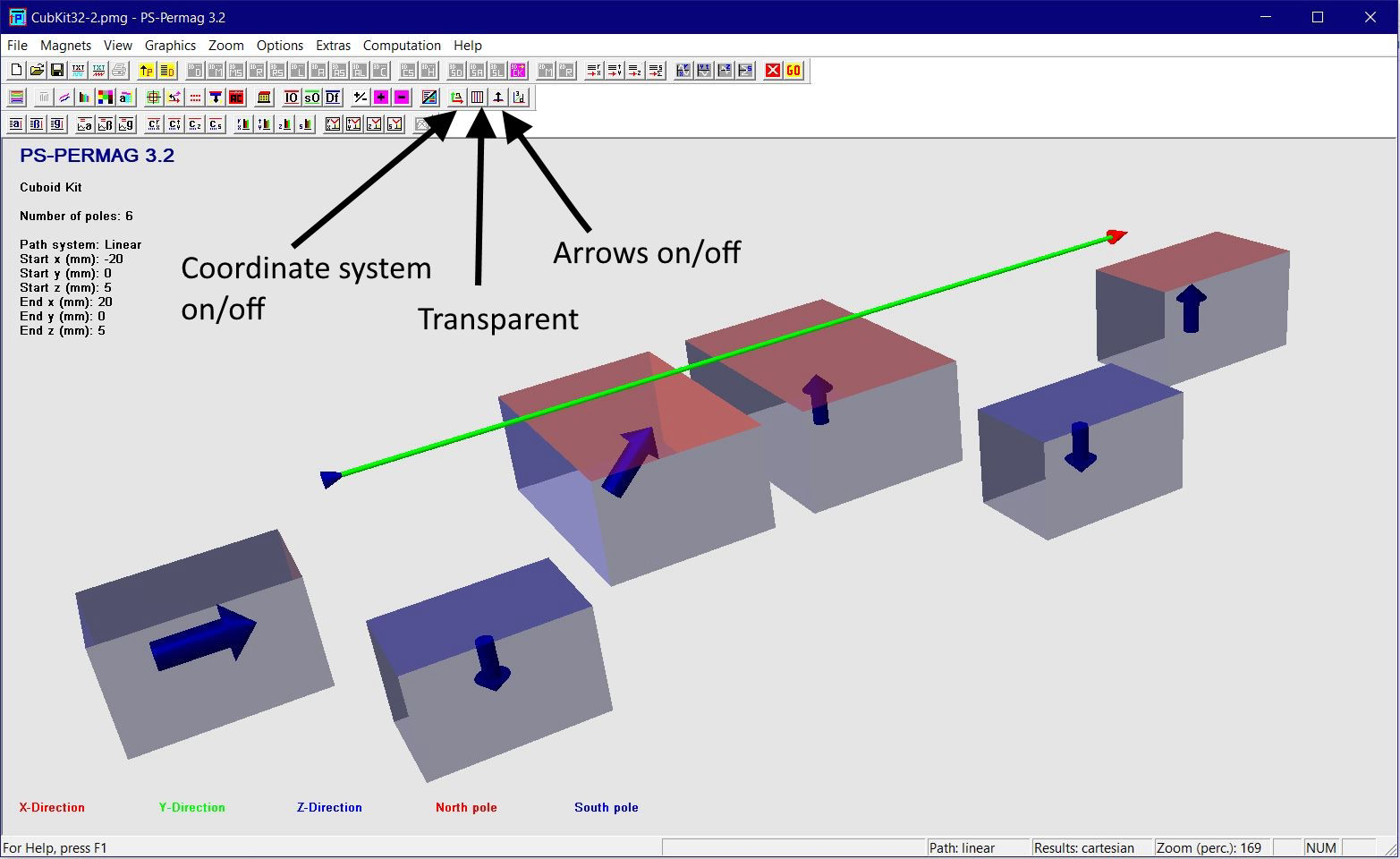
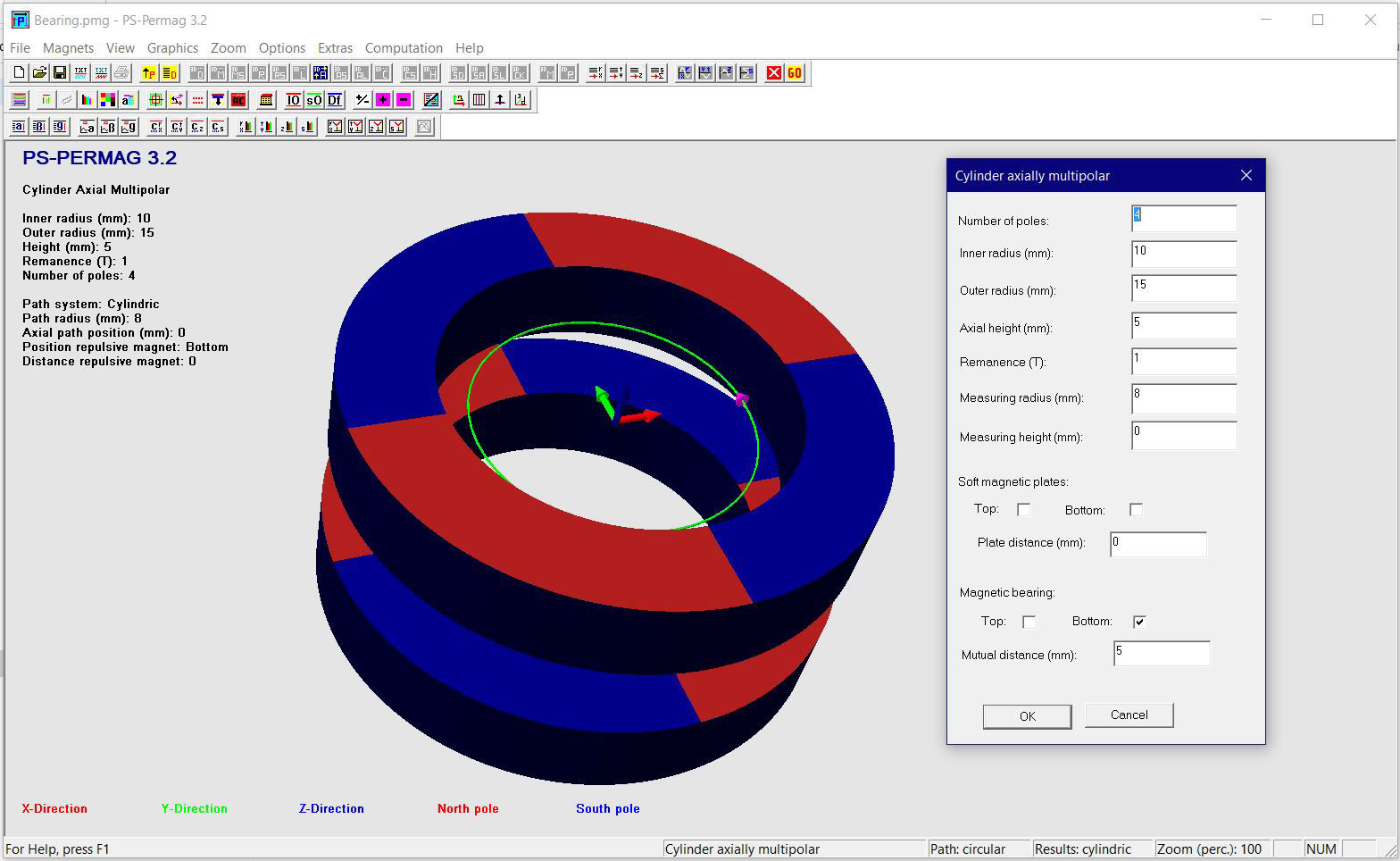
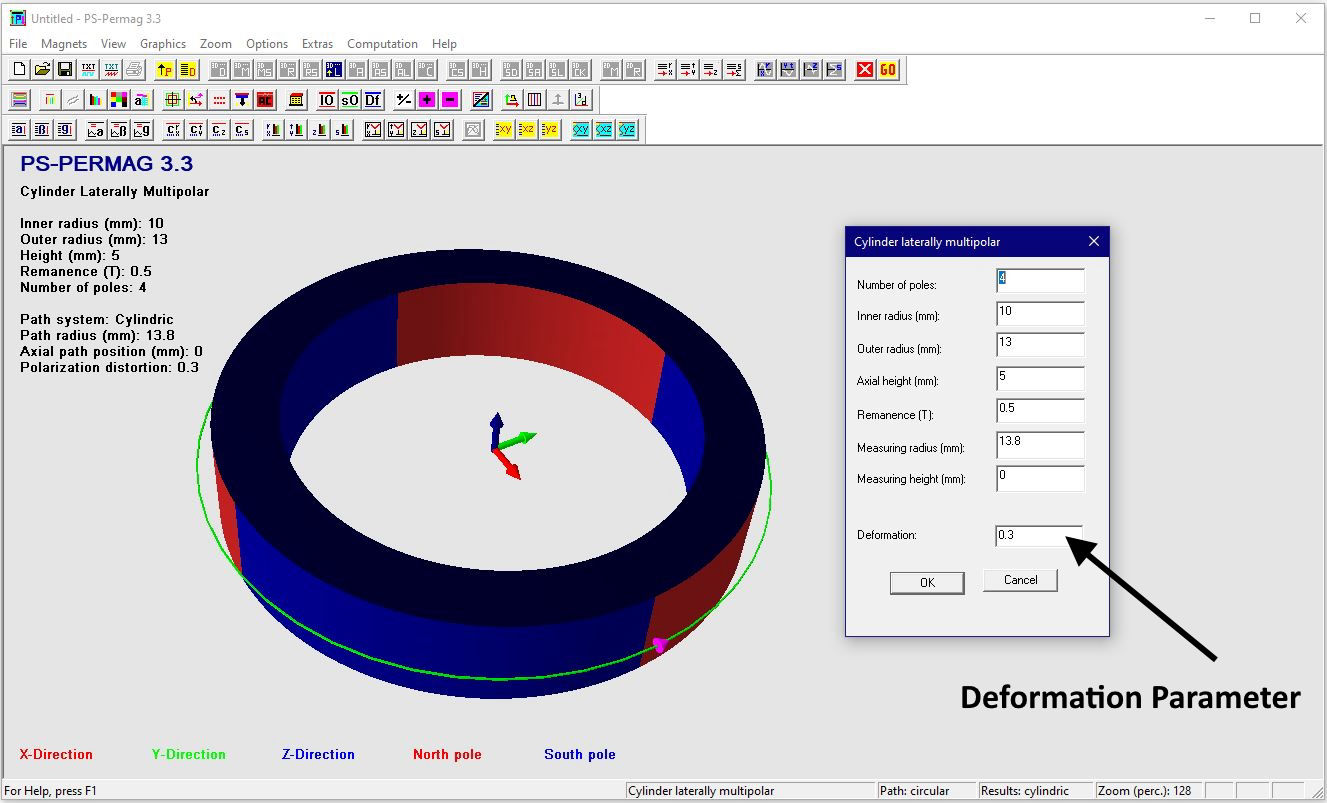
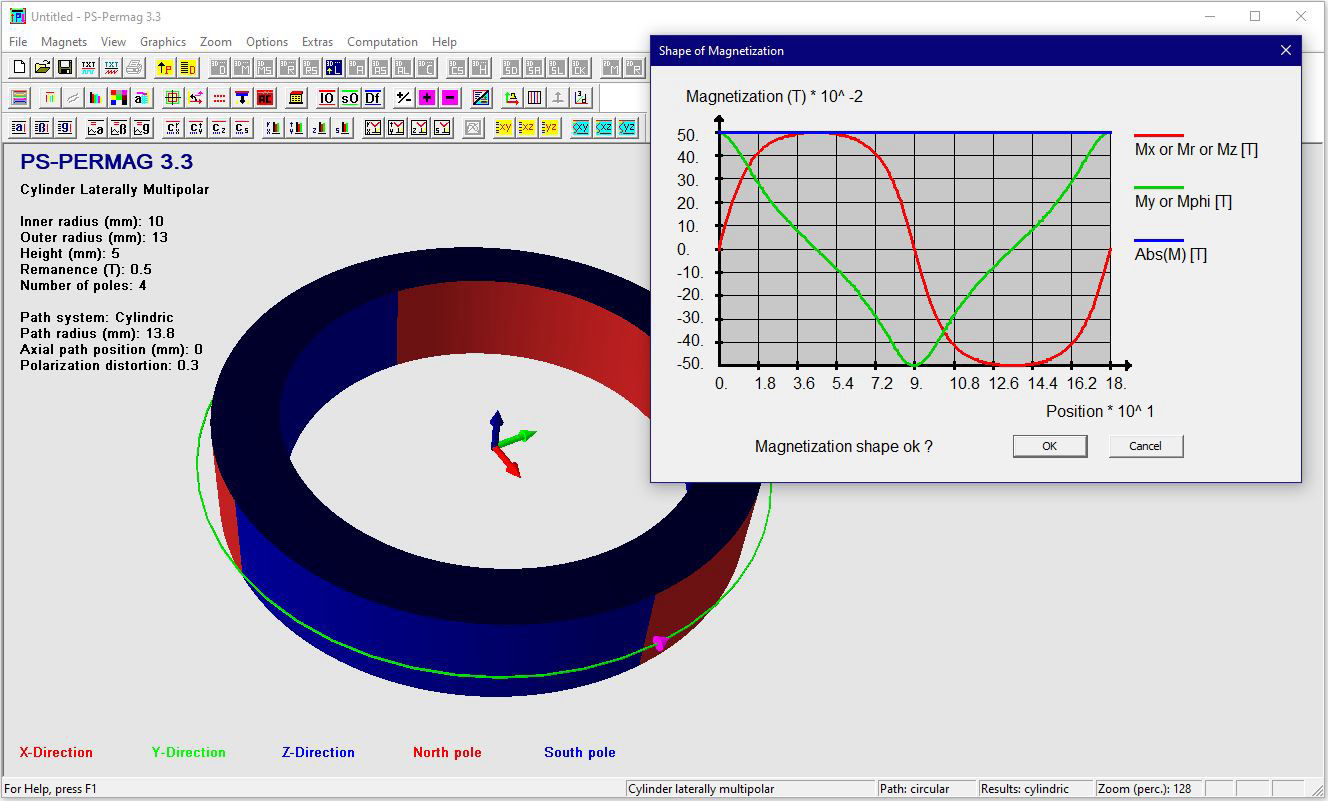
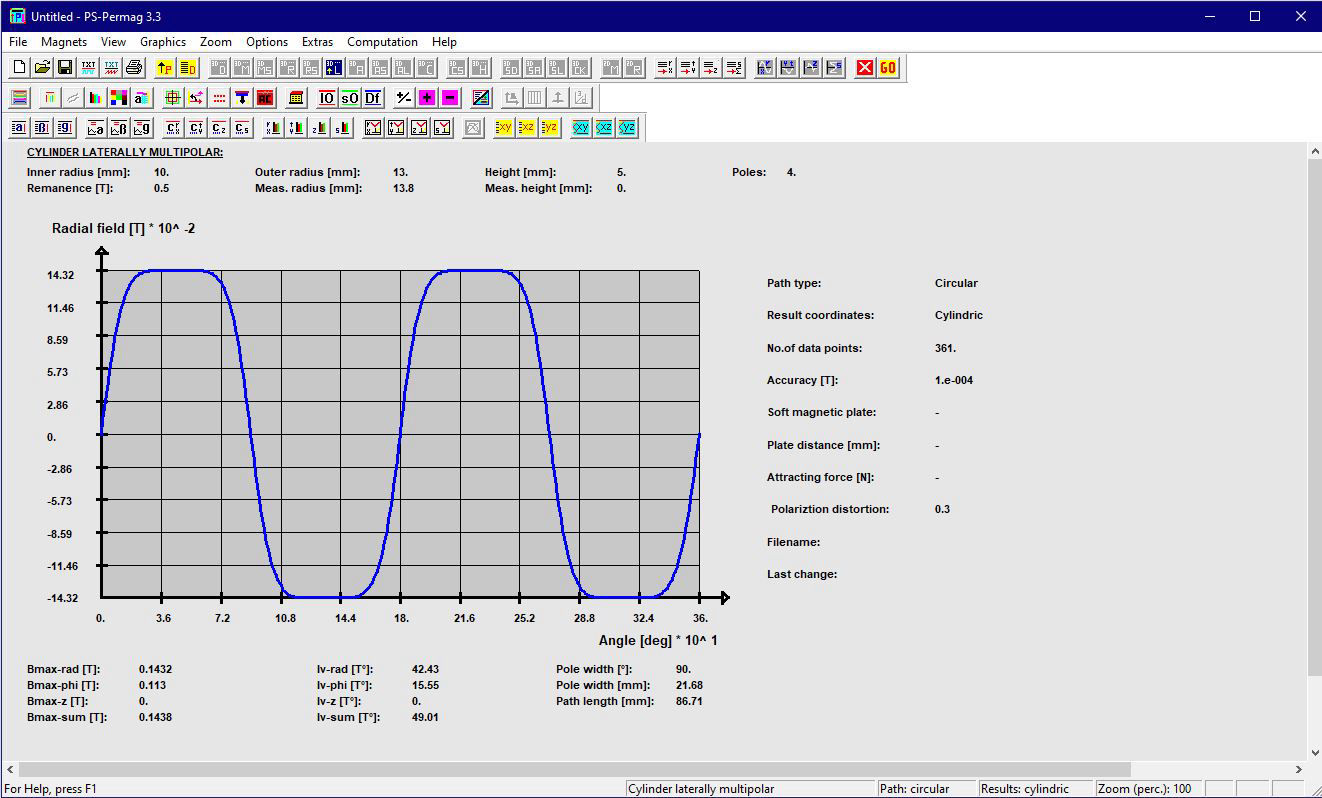
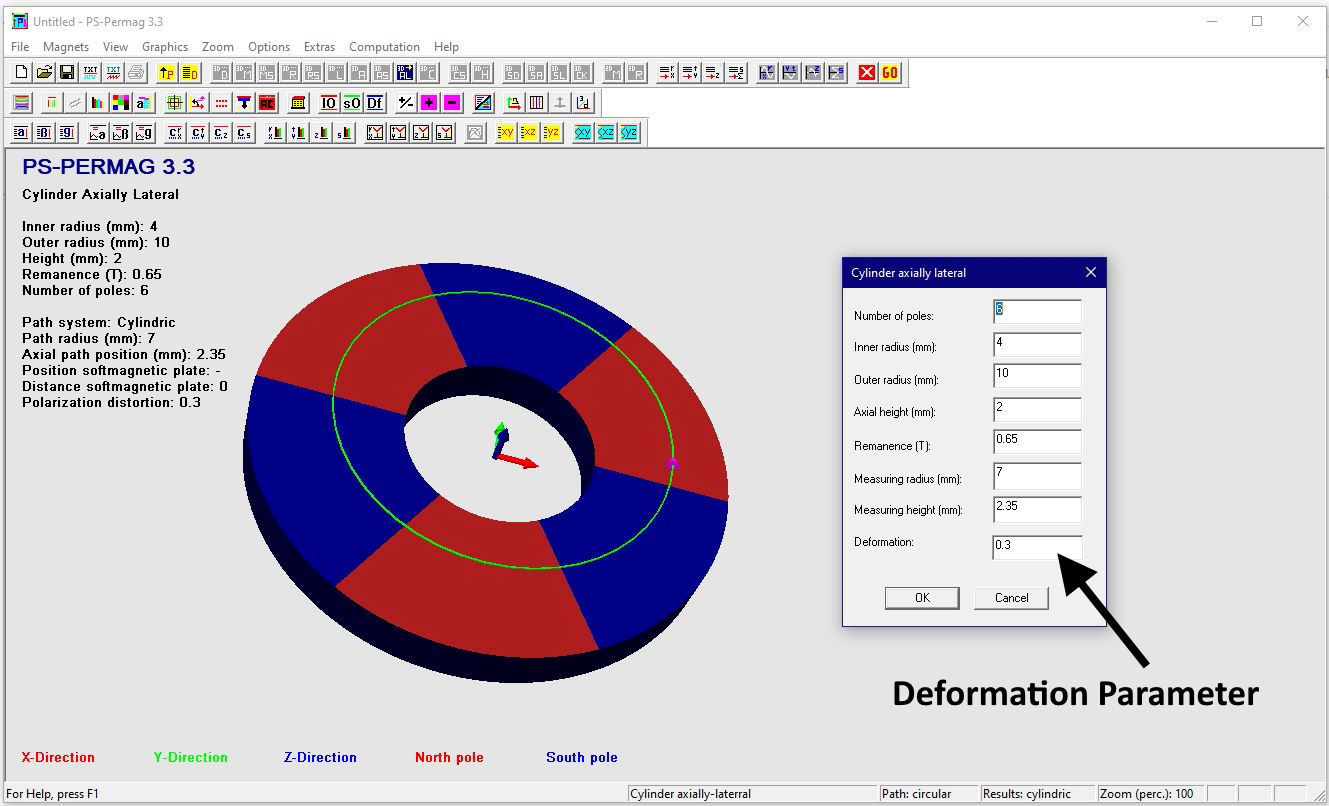
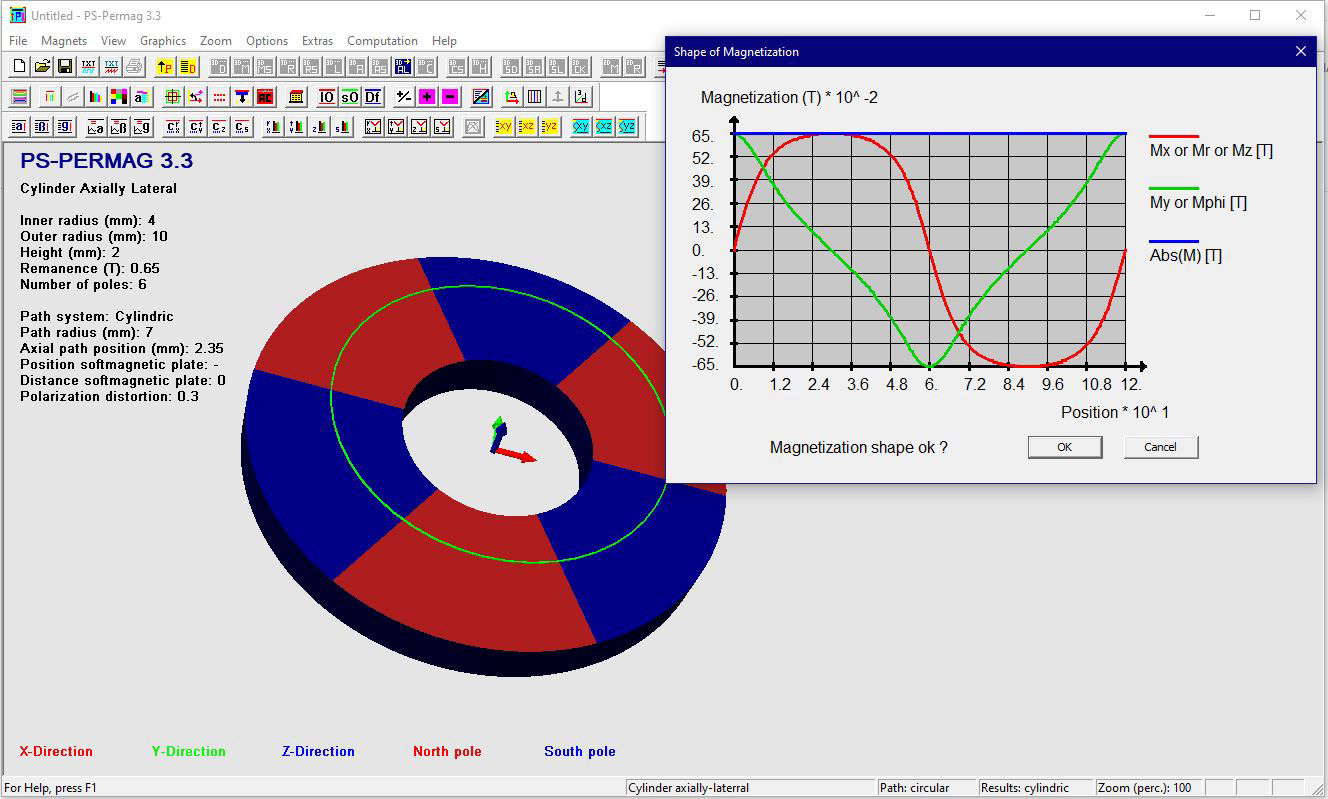
Dieses Tutorial zeigt die grundlegende Handhabung von PS-PERMAG sowie dessen Eigenschaften. Das Berechnungsproblem besteht hier in einem aus sechs anisotropen Ferritsegmenten hergestellten Zylinder, wobei jedes Segment eine Remanenzinduktion von 0.40T aufweist. Das Tutorial zeigt die Bedienung hier anhand der Version 3.0. Das unten stehende Beispiel sowie ähnliche Probleme lassen sich auch mittels der aktuellen Demoversion von PS-PERMAG und natürlich auch mit der Vollversion von PS-PERMAG3.1 ausführen. Die in diesem Tutorial nicht explizit gezeigten Features sind außerdem leicht anhand des ausführlichen Hilfesystems der Software erlernbar. Das Tutorial 3.1 weiter unten zeigt die Eingabe von zusätzlichen Vertiefungen und Rändern bei zweipoligen Sensormagneten, welche in Vers. 3.1 neu eingefürt wurden.

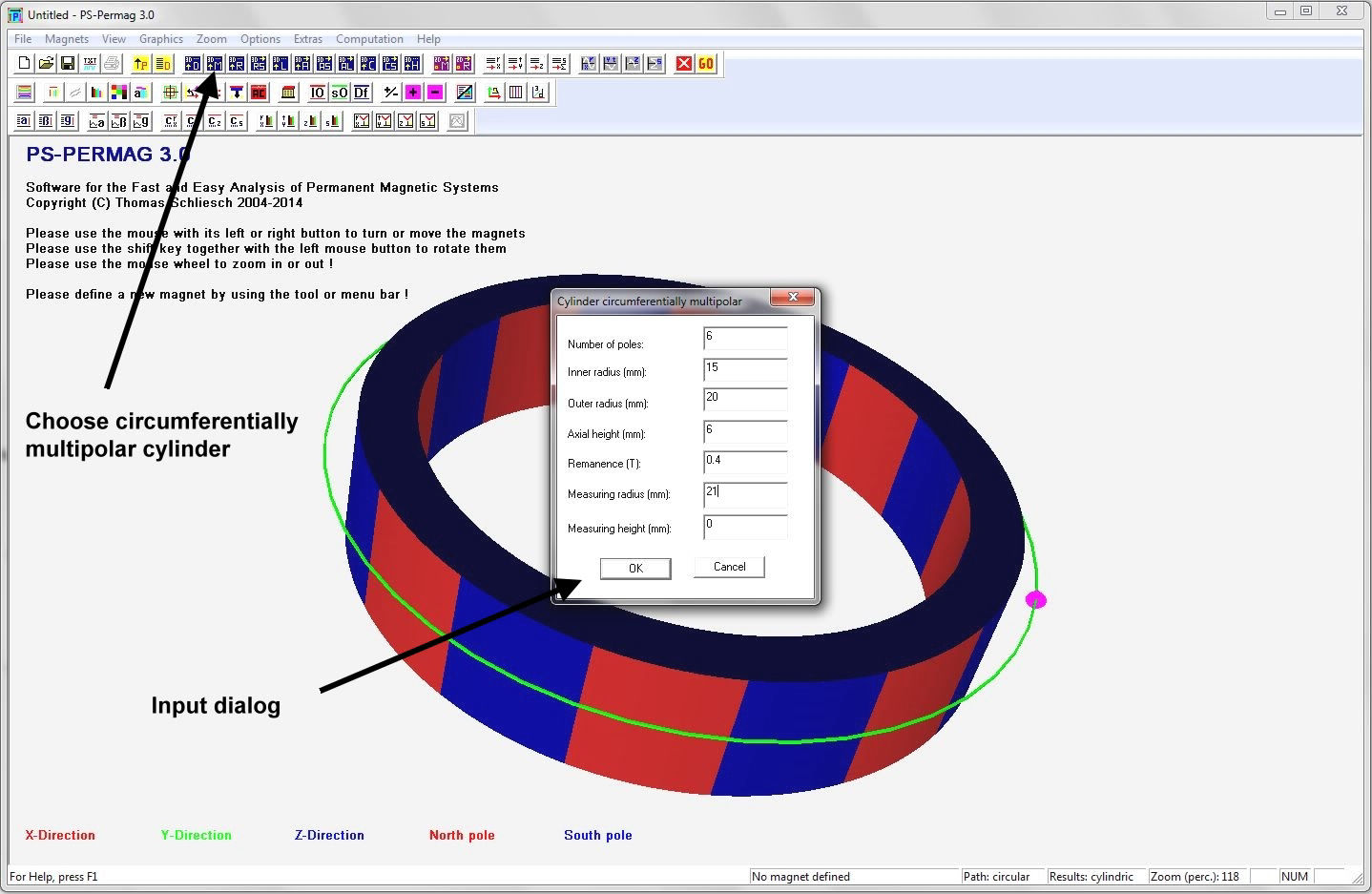
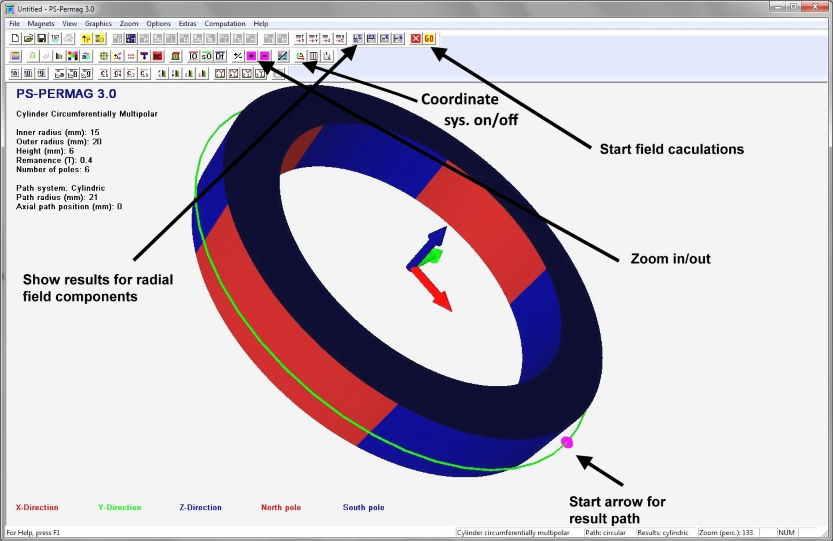
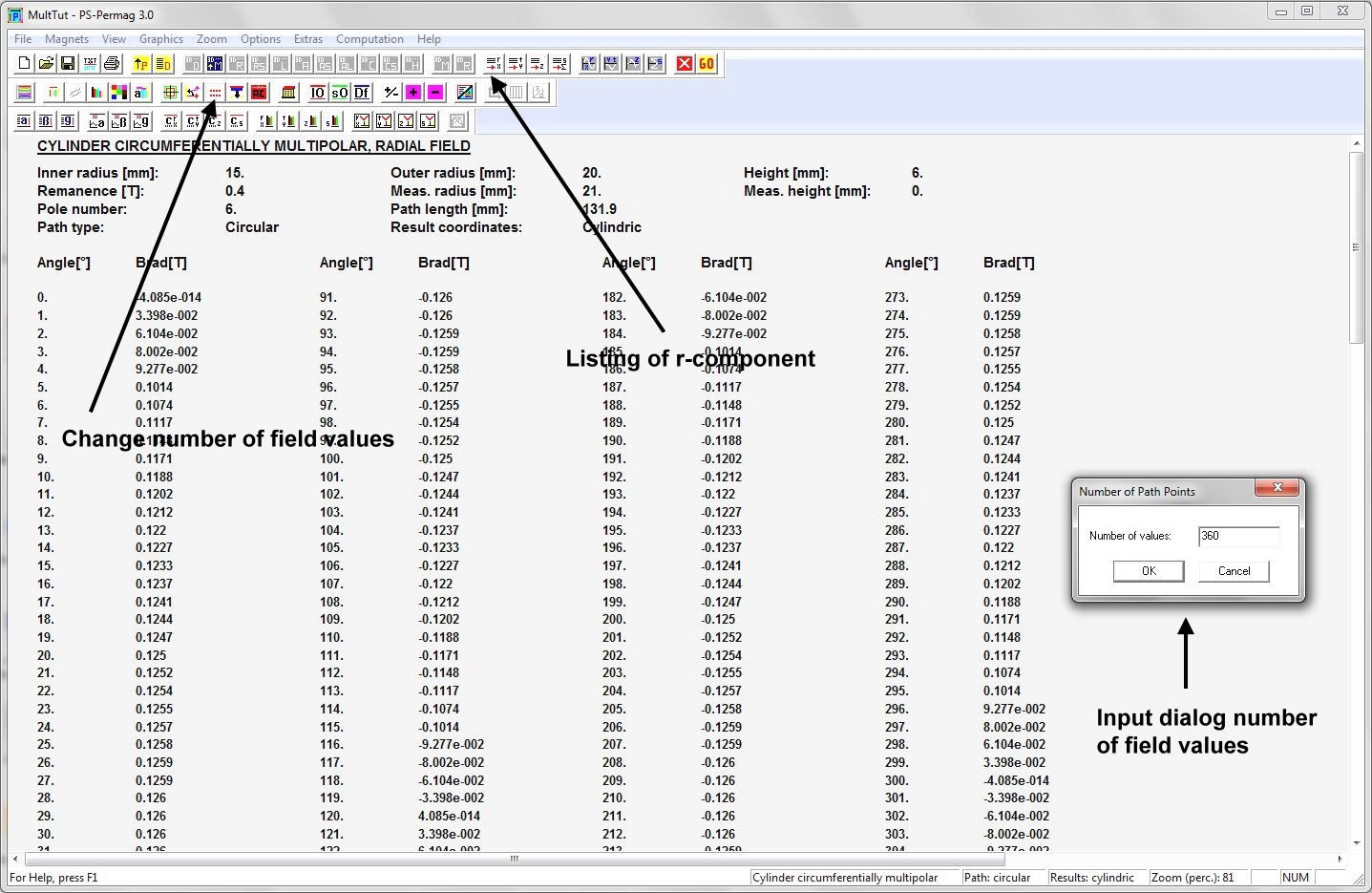
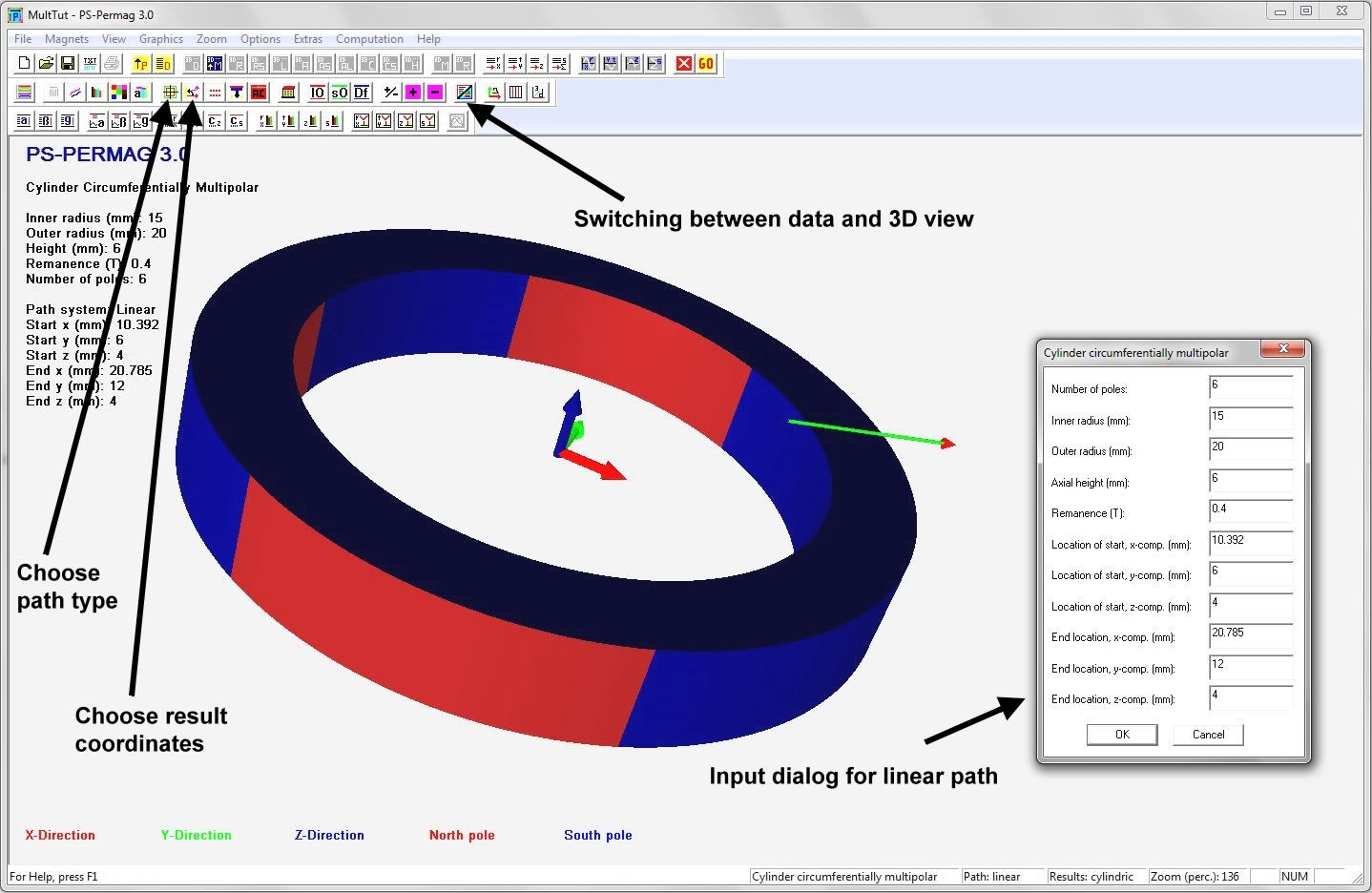
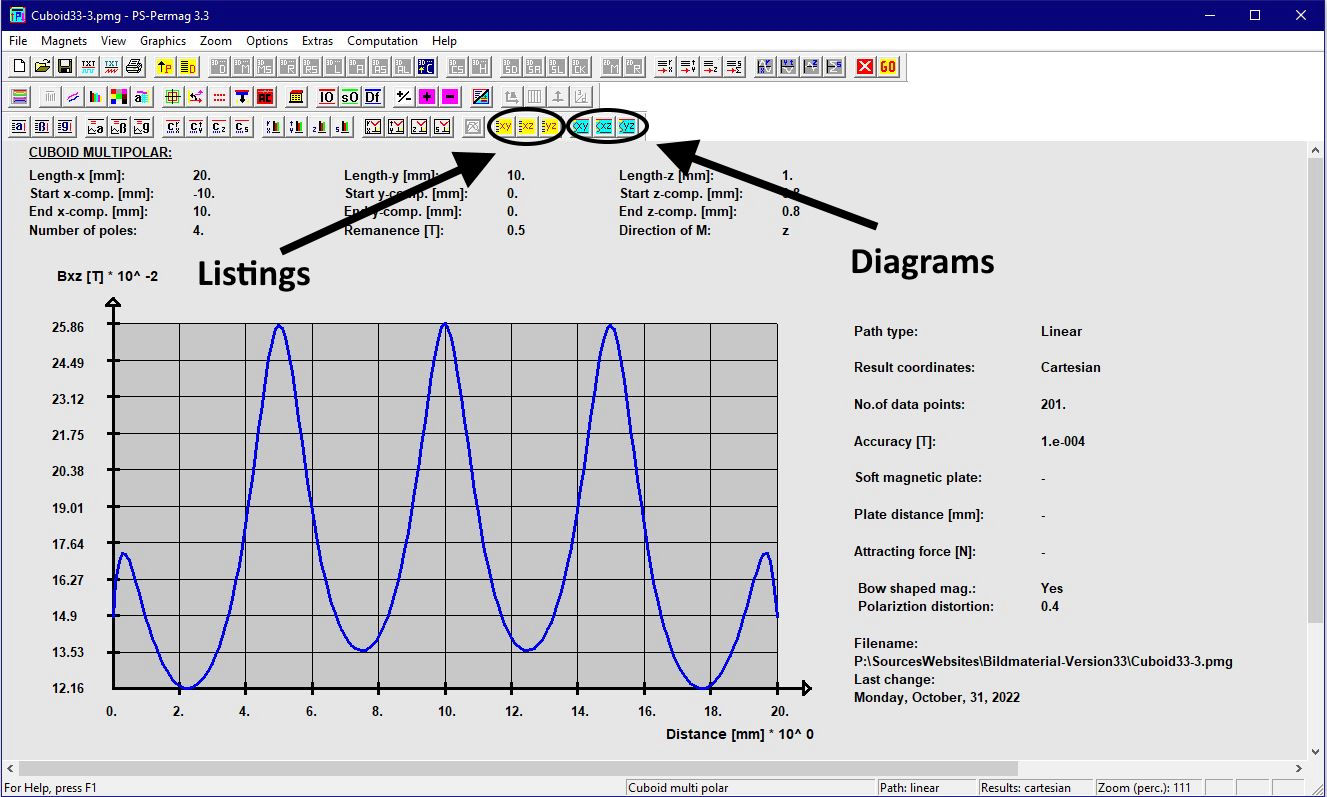
Nach dem Programmstart von PS-PERMAG erscheint zur Illustration ein 3D-Modell eines Dauermagnetzylinders. Zur Definition eines neuen Magneten klicken Sie bitte auf das M-Symbol in der oberen Symbolleiste der Software, welches für am Umfang multipolar homogen magnetisierte Zylindermagnete steht, siehe nächstes Bild. Dies öffnet einen entsprechenden Eingabedialog, in den die grundlegenden Parameter für diesen Magneten eingegeben werden. Basis für die Eingabe der Magnetparameter ist im Fall von Zylindermagneten ein zu diesen symmetrisches zylindrisches Koordinatensystem. Dies bedeutet zum Beispiel, dass auf halber axialer Höhe des Magneten immer z=0 ist. Beim Winkel phi=0 beginnt jeweils immer ein nach außen weisender Nordpol.

Nachdem Sie OK gedrückt haben erscheint das Unten dargestellte 3D-Modell des definierten Magneten inklusive des gewählten Ergebnispfades. Sie können dies mittels des Mausrades vergrößern oder verkleinern, mittels Linksklick und Bewegen der Maus um die x- oder y-Achse drehen und mittels gedrückter rechter Maustaste horizontal oder vertikal verschieben. Gleichzeitiges Drücken von linker Maustaste und Shifttaste auf dem Keyboard führt zu einer Drehung des Magneten um die z-Achse. Eine generelle Methode zur Vergrößerung oder Verkleinerung der Bildschirmdarstellung besteht auch in der Betätigung des + oder - Buttons in der zweiten Symbolleiste des Programms. Hiermit lassen sich neben den 3D-Modellen sämtliche weitere Bildschirminhalte in ihrer Größe verändern. Mittels des benachbarten Symbols SO können die entsprechenden Zoomfaktoren für die Darstellung von Texten und Diagrammen als Voreinstellung für weitere neue Berechnungen gespeichert werden, womit eine generelle Anpassung an die Bildschirmauflösung des Users möglich ist. Das Koordinatensystem können Sie mit dem entsprechenden Symbol in der 2. Symbolleiste an und ausschalten. Drücken Sie nun den GO-Button zum Start der Feldberechnung. Nach einigen Sekunden sollte diese erfolgt sein; der Fortschritt wird mittels eines entsprechenden Balkens angezeigt. Drücken Sie dann den entsprechenden Button zur Anzeige der radialen Feldkomponente auf dem Ergebnisfad. Dieses Symbol sollte die Buchstaben r und x beinhalten. Die drei rechts benachbarten Symbole stehen für die graphische Darstellung der übrigen Feldkomponenten sowie des Feldbetrages.

Wir kommen nun zur Betrachtung der ersten Resultate, hier in Form des radialen Feldes als Funktion des Umlaufwinkels. Anstatt den vollen Bereich des Feldes wiederzugeben, kann man den Winkelbereich oder Streckenbereich auch einschränken. Hierzu klicken Sie bitte auf das entsprechende Symbol auf der linken Seite in der zweiten Symbolleiste (Options Bar), womit sich ein entsprechender Eingabedialog öffnet. Möchten Sie zum 3D-Model des Magneten zurückkehren, so drücken Sie bitte den entsprechenden Knopf in der rechten Hälfte der zweiten Symboleiste. Rechts neben diesem befinden sich (hier angegraut) drei Knöpfe für Optionen zur 3D-Darstellung (Ausschalten Koordinatensymbol, transparente Magnetdarstellung, Voreinstellung der Magnetposition).

Die Felder können natürlich auch in der Form von Zahlenkolonnen dargestellt werden, wozu man auf die entsprechenden hellgrauen Symbolknöpfe in der ersten Symbolleiste klickt. Der erste dieser Knöpfe öffnet die entsprechenden Liste für das radiale Feld im Fall zylindrischer Ergebnisskordinaten. Im Fall von kartesischen Koordinaten wird in der Tabelle die x-Komponente aufgelistet. Generell sollte für einen zylindrischen Magneten zur Ergebnisausgabe ein zylindrisches Koordinatensystem voreingestellt sein. Allerdings lässt sich für alle Magnete die Ausgabe auch in kartesische Koordinaten ändern. Durch Anklicken des entsprechende Buttons mit den zwei gepunkteten Linien in der zweiten Symbolleiste, wie unten per Pfeil spezifiziert, kann man die Anzahl der berechneten Werte pro Pfad verändern. Anschließend ist dann eine Neuberechnung der Felder notwendig.

Zusätzliche Auswertungen, die auf die errechneten Feldwerte basieren, sind zum Beispiel Fouriereihen-Entwicklungen von periodischen Feldkonfigurationen. Im Fall dass eine graphische Übersicht über eine derartige Approximationen z.B. für das r-Feld gewünscht wird, klicken Sie bitte in der dritten Symbolreihe (Evaluation Bar) auf das erste graue Symbol aus der letzten Vierergruppe. Darauf wird die Originalkurve der r-Komponente zusammen mit einer Annäherung durch Fourierreihen unterschiedlicher maximaler Ordnung angezeigt. Unten ist dies für die ersten beiden Pole des Magneten nach Einschränkung der graphischen Anzeige auf 180° dargestellt. Welche und wie viele Ordnungen dargestellt werden, kann durch Klick auf den ersten Knopf in der zweiten Symbolreihe bestimmt werden. Eine numerische Liste aller Fourierkoeffizienten kann für die jeweilige Feldkomponente durch Klicken auf das entsprechende mit c gekennzeichnete Symbol in der dritten Symbolreihe angezeigt werden, wie unten per Pfeil spezifiziert. Des weiteren lässt sich die Verteilung der unterschiedlichen Ordnungen auch graphisch darstellen, siehe das durch Pfeil entsprechend markierte Symbol in der vorletzten Vierergruppe der unteren Symbolleiste. Neben den drei Feldkomponenten lässt sich auch der Absolutbetrag des Feldes in seiner Fourierreihenentwicklung analysieren.

Eine weitere mögliche Auswertung der Feldkomponenten bezieht sich auf die Feldwinkel, deren Kenntnis zum Beispiel in der Sensortechnik von Relevanz ist. Mittels der untersten Symbolreihe kann durch das Anklicken eines der Knöpfe aus der zweiten Dreiergruppe der jeweilige Verlauf des Feldwinkels als Funktion des geometrischen Winkels (bei Zylinderkoordinaten) oder als Funktion der Ortsposition (bei kartesischen Koordinaten) graphisch dargestellt werden. Im Bild unten ist zum Beispiel der Winkel der Feldprojektion in der r-phi-Ebene als Funktion des Pfadwinkels gezeichnet. Die erste Dreiergruppe von Buttons in der unteren Symbolreihe ermöglichen das jeweilige numerische Listing. Alle Winkel sind zwischen -180grad und +180grad definiert. Graphikfarben können generell durch Klick in der Optionsleiste und im anschließenden Dialog gewählt werden, wie ebenfalls im Bild unten gezeigt wird.

Neben kreisförmigen Pfaden sind auch geradlinige Pfade im Raum, auf denen sich die Feldkomponenten berechnen lassen, für alle Magnettypen definierbar. Des weiteren können alle Resultate auf allen Arten von Pfaden sowohl in zylindrischen als auch kartesischen Koordinaten berechnet werden. Im unten stehenden Bild sind die Wahl der entsprechenden Buttons für den Wechsel der Pfadgeometrie als auch für die Auswahl eines Ergebniskoordinatensystems mit Pfeil gekennzeichnet. Betätigt man den entsprechenden Button für die Problemdefinition und hat statt eines kreisförmigen Pfades einen linearen Pfad gewählt, so wird ein Eingabedialog wie in der Abbildung unten geöffnet. In den 3D-Modus so wie er unten dargestellt ist, kommen Sie wieder mit dem Umschaltbutton in der zweiten Symbolleiste. Der lineare Pfad ist hier oberhalb des ersten Pols als grüne Linie sichtbar. Im unten stehenden Fall soll der Pfad 1mm oberhalb des ersten Pols zwischen dem Radius r=12mm bis r=24mm verlaufen, und zwar genau oberhalb der Polmitte. Für geradlinige Pfade sind stets die kartesischen Koordinaten des Start- und Endpunktes einzugeben. Da sich die Polmitte des ersten Pols bei 30° befindet sowie für die Magnethöhe der Wert hm=6mm gilt, so ergeben sich für die einzelnen Koordinaten des Anfangs-Punktes die folgenden Werte x=12*cos(30)=10.392, y=12*sin(30)=6.0, z=hm/2+1=4.0. Für die Werte des Endpunktes des Pfades gelten: x=24*cos(30)=20.785, y=24*sin(30)=12.0, z=hm/2+1=4.0. Nach Eingabe wird mittels des Go-Buttons wie oben die entsprechende Berechnung gestartet.

Im nächsten Screenshot ist das Resultat der x-Komponente des Feldes nach Eingabe wie in der obigen Abbildung sowie nach zusätzlichem Wechsel der Ausgabekoordinatensystems auf kartesische Koordinaten abgebildet. Wegen des linearen Pfades werden die Felder nun als Funktion der Wegstrecke ausgegeben.

Zum Abschluß dieses Tutorials sollten noch einige weitere Möglichkeiten der Software erwähnt werden (Version 3.0): Durch Klick in der oberen Symbolreihe kann ein Dialog zur Texteingabe einer Beschreibung der laufenden Analyse geöffnet werden. Neben dem üblichen binären Speichern der primären und sekundären Analyseresultate, welches auch eine Vielzahl der momentanen Programmeinstellungen umfasst, besteht auch die Möglichkeit durch Klick auf das “txt”-Symbol die Felder als ASCII-File zu exportieren Ein anderer wichtiger Button ist in der ersten Symbolreihe der rote Knopf neben dem “Go”-Symbol, welcher einen Abbruch der laufenden Berechnung ermöglicht. In der Optionsleiste sind in Ergänzung zu den bisher erwähnten Möglichkeiten Dinge wie das Ändern der Rechengenauigkeit oder die Eingabe und Speicherung der wichtigsten User-Daten möglich, welche dann in den ausführlichen Ausdrucken von PS-PERMAG stets mit angegeben werden. Die Größe von Schrift und Graphiken kann einerseits durch Bedienung der + und - Buttons den jeweiligen Bedürfnissen des Anwenders angepaßt werden. Des weiteren sind die Schrift- und Kurvenstärke sowie die Darstellung der Diagrammgitter mittels eines weiteren Buttons in der Optionsleiste festlegbar. Drei Sorten von Symbolknöpfen zur Speicherung und Wiederherstellung der Grundeinstellungen der Software stehen in der Optionsleiste ebenfalls zur Verfügung. Nicht zu vergessen ist, dass alle Symbole auch ihre Entsprechung in einem jeweiligen Menübefehl haben. Die Menübefehle sind mittels der Menüleiste ganz oben im Programmfenster zugänglich. Weitere Programmfeatures können Sie mittels des ausführlichen Hilfesystems der Software leicht erlernen.

Tutorium 3.1

Lernen Sie hier die neuen Features von Version 3.1 kennen und handhaben. Dies betrifft im Detail drei neuen Arten von zweipoligen Sensormagneten mit Vertiefungen und Rändern.

Eingabe eines zweipolig axialen Sensormagneten mit Vertiefungen und Rändern

Dieses Tutorial zeigt die Eingabe der Geometrie bei den in der Version 3.1 neu hinzugekommenen zweipoligen Sensormagenten die Vertiefungen oder Ränder aufweisen. Die grundsätzliche Bedienung von PS-PERMAG können Sie im Tutorial 3.0 erlernen.

Im Folgenden behandeln wir einen zweipolig axialen Sensormagneten. Die Eingabe der Geometrie der beiden anderen Arten entsprechenden Sensormagnete, d.h. zweipolig diametral und einseitg axial-lateral erfolgt analog. Definieren Sie zuerst einen Zylinder, von dem die Ränder oder Vertiefungen mit bis zu vier Hilfsvolumina später subtrahiert werden können, siehe Abbildung.

Eine Vertiefung auf der Oberseite wird dann durch Angabe des Radius und der Höhe mittels des Hilfsvolumens V1 definiert, wie in der nächsten Abbildung gezeigt.

Sollte auf der Oberseite ein äußerer Rand definiert werden, so wird dazu das Hilfsvolumen V2 verwendet. Der Radius r2 gibt hierbei die radiale Breite gerechnet vom äußeren Rand des Basiszylinders an.

Sollte auf der Unterseite eine mittige Vertiefung benötigt werden, so kann hierzu das Volumen V3 verwendet werden, wie in der unten stehenden Abbildung gezeigt ist.

Schließlich kann, wenn gewünscht, auch auf der Unterseite ein vertiefter Rand definiert werden und zwar mittels des Volumens V4. Hier entspricht der Radius wieder der radialen Länge ab dem äußeren Rand des Basiszylinders.

Drehbare Ergebnis-Koordinatensysteme

In Version 3.2 wurde für alle Magnetarten die Möglichkeit eingeführt gedrehte Ergebnis-Koordinaten zu verwenden. Dabei können Drehwinkel um die Basisachsen des jeweils verwendeten kartesischen oder zylindrischen Koordinatensystems eingegeben werden. Dies ist u.A. wichtig bei magnetischen Sensorsystemen. Hier können gerinfügige Fehlstellungen bei der Sensormontage oder Toleranzen in den Sensorchips von nur wenigen 0.01mm zu größeren Positionsfehlern führen. In der unten stehenden Abbildung ist die Eingabe eines um 5° um die radiale Achse des Zylinderkoordinatensystems verdrehten Koordinatensystems dargestellt.

Befindet sich der Sensor aufgrund von Systemtoleranzen auf einem Radius von 1mm von der Drehachse, so wird die Verkippung des Sensors um 5° hier zu erheblichen Fehlern bei der Bestimmung des Drehwinkels um mehrere Grad führen, wie z.B. durch die markierten Zahlenwerte im nachfolgend dargestellten Listings des magnetischen Winkels entnehmbar ist.

Cuboid-Baukastensystem

Mittels des Cuboid-Baukastens lassen sich Anordungen von Magnetblöcken unterschiedlicher Position, Größe sowie mit unterschiedlicher Stärke und Richtung der Magnetisierung definieren. Nachfolgende Abbildung zeigt ein entsprechendes Beispiel hier mit einem linearen Ergebnispfad

Nachfolgender Dialog zeigt eine typische Eingabemaske für ein derartiges System. Dabei werden die einzelnen Blöcke mittels des Ortes der unteren linken Ecke im kartesischen Koorinatensystem definiert sowie mittel deren Längenausdehung in x-, y-und z-Richtung. Die jeweiligen Richtung der Magnetisierung wird dabei durch den Polarwinkel mit der z-Richtung (0-180Grad) sowie mittels des Azimutwinkels (0-360Grad) definiert.

Hier ist ein weiteres Beispiel für ein mit dem Cuboid-Baukasten definiertes System. Da hier willkürliche Richtungen den Magnetisierung definiert werden können, besteht für diese Problemart die Möglichkeit in der 3D-Ansicht die Richtungen mittels entsprechender Pfeile anzuzeigen. Dies erfolgt bei Aktivierung des Transparenz-Modus mit dem entsprechenden Knopf in der Optionsleiste. Die Pfeile können dabei an- und ausgeschaltet werden. Stört dabei das Symbol für das Koordinatensytem, so lässt sich dies natürlich mit dem entsprechenden Button links from Transparenz-Symbol deaktivieren. Die Pfleisymbole zeigen nur die Richtung, jedoch nicht die jeweilige Stärke der Magnetisierung an.

Axiale Magnetlager

Axiale Magnetlager mit beliebiger Polzahl lassen sich als neues Feature bei der Definition von mehrpolig axialen Magneten definieren. Dabei kann nun ausgewählt werden, ob der definierte Magnet sich gegenüber einer magnetisch leitenden Platte oder gegenüber einem gleichartigen jedoch entgegengesetzt gepolten Zwillingsmagneten befindet. Der nachfolgende Screenshot zeigt ein vierpoliges Magnetlager wobei im Eingabedialog hier ein gegenseitiger Abstand von 5mm eingegeben wurde. Die Software gibt nach Berechnung des Feldes unabhängig vom gewählten Feldpfad die Abstosskraft wieder.

Lateral bogenförmig am Umfang magnetisierte Magnete mit variabler Polform

Lateral am Umfang magnetisierte Magnete (L-Symbol in der Symbolleiste) weisen in der Voreinstellung eine sinusförmige Magnetisierung mit nach Innen abnehmendem Betrag auf. Die resultierenden Felder zeigen daher keine höher harmonischen Fourieranteile. Andererseits ist es für bestimmte Anwendungen sinnvoll eine eher trapezoidale Magnetisierung anzunehmen. Alle Arten der Feldform zwischen ideal sinsusförmig und nahezu starr radial können daher mit dem neu eingeführten sogenannten Deformationparameter modelliert werden. Diese Polarisationenformen entsprechen den mit den üblichen Fertigungsferfahren der Magnettechnik herstellbaren Konfigurationen von Permanentmagneten (mit der Ausnahme von nachträglich assemblierten Einzelpolen). Der Deformationsparameter kann kontinuierlich zwischen 0 (ideale Sinusform) und 1 (radiale Magnetisierung mit marginaler Übergangszone) varriert werden. Die nachfolgende Abbildung gibt die Eingabemaske eines lateral am Umfang magnetisierten Magnetenringes wieder mit dem neu für diesen Magnettyp eingeführten Defomationsparameters:

Wird ein Deformationsparameter > 0 eingegeben, so öffnet sich ein Diagramm welches die Verteilung der radialen und tangentialen Komponente der Magnetisierung an der Magnet-Oberfläche sowie den Betrag der Magnetisierung wiedergibt. Hiermit kann der Grad der Abweichung von einer ideal sinusförmigen Polarisation bzw. die Größe der Übergangszone zwischen den Polen wiedergegeben werden. Bei lateral am Umfang magnetisierten Magneten erfolgt dies immer für ein Polpaar, welches sich im Fall des hier vierpoligen Magneten über einen Winkel von 180° erstreckt. Im nachfolgenden Bild beträgt der Deformationsparameter 0.3.

Die nachfolgende Abblildung gibt die Verteilung des radialen Feldes nahe der Magnetoberfläche des obigen Magneten wieder. Deutlich wird die Abweichung von einer Sinusform durch die deformierte Verteilung der magnetischen Polarisation.

Axial-Laterale Zylindermagnete mit variabler Polform

Abweichungen von einer sinusförmigen Polarisation mittels eines Defomationsparameters sind in Version 3.3 analog auch für axial bogenförmig polarisierte Zylindermagnete eingeführt worden. Nachfolgende Abbildung zeigt die entsprechende Eingabemaske, hier ebenfalls mit dem Deformationsparameter 0.3 bei einem sechspoligen Magneten.

Die nächste Abbildung gibt die entsprechende Verteilung der Polarisationskomponenten an der Oberfläche sowie den Absolutbetrag wieder. Ein Polpaar entsricht wegen der sechs Pole hier 120°

Die Auswirkungen auf das axiale Feld nahe der Magnetoberfläche werden im nachfolgenden Bild anhand einiger Fourierreihen-Entwicklungen bis zu gewissen Ordnungen angezeigt. Die Abweichungen von einer ideal sinusförmigen Polarisation führen zu einem Klirrfaktor von ca. 9% wie durch die Zahlenangabe rechts unten ersichtlich.

Multipolare Quadermagnete mit bogenförmiger Magnetsierung und variabler Feldform

Eine zusätzliche bogenförmige Magnetisierung mit variabler Feldform für multipolare Magnetquader (C-Option in der Auswahl-Symbolleiste) wurde nun in Version 3.3 implementiert. Bis Version 3.2 konnten Cuboide nur mit starrer alternierender Magnetisierung behandelt werde. Die Neuerung zeigt das nachfolgende Bild, bei dem durch Setzen einer Markierung im entsprechenden Eingabe-Feld von der starren Magnetisierung in eine bogenförmige Magnetisierung umgeschaltet werden kann. Ist die Markierung gesetzt, so bedeutet eine 0 beim nachstehenden Deformationsparameter wieder eine ideal sinusförmige Polarisation, während höhere Werte Abweichungen hiervon definieren. Ist der Deformationsparameter 1 so ergibt sich eine nahezu perfekte axiale Magnetisierung mit einer nur noch geringfügigen Übergangszone zwischen den Polen. Die Magnetisierung nimmt bei den bogenförmigen Polformen entsprechend der Verhältnisse bei einer realen Impulsmagnetisierung langsam von oben ins Magnetinnere ab. Ist keine Haken bei der bogenförmigen Magnetisierung gesetzt, so hat der Deformationsparameter keine Auswirkungen.

Die Abbildung hebt zusätzlich die Buttons für das Listing und die Diagramme der Vektorsummen in den Koordinatenebenen hervor, die anhand eines Beispiels im nächsten Unterabschnitt behandelt werden und in der Version 3.3 für alle Magnetarten eingeführt wurden.

Nachfolgendes Bild gibt die Verteilung der Magnetisierungs-Komponenten bei einem Faktor von 1 an. Bei den Quadermagneten wird ein entsprechendes Diagram nur über einen Pol angezeigt. Die Übergangszone zu den Nachbarpolen ist im abgebildeten Fall nur noch geringfügig klein, so wie es z.B. bei einer Impulsmagnetisierung von realen Magneten auftreten würde. Soll eine ideal starre Magnetsierung ohne Übergangszone modelliert werden, so ist der Haken für die bogenförmige Polarisation zu entfernen.

Nachfolgendes Diagram zeigt die Bz-Komponente des Feldes nahe der Magnnetoberfläche entlang des oben abgebildeten Pfades nach jeweiligem Export in ein Tabellen-Kalkulationsprogramm. Dabei wurde die bogenförmige Magnetisierung mit den Deformationsparameters 0, 0.25, 0.4 und 1.0 modelliert. Das Resultate bei der ideal starren Magnetisierung ist ebenfalls mit angegeben.

Feldbetrag in Koordinatenebenen

Die Ausgabe von Feldbeträgen aus nur zwei Komponenten ist besonderes für die Magnetsensor-Technik relevant, da dann meist nur die Komponenten in einer Ebene ausgewertet werden. Für jeden Pfad sind dies entweder die kartesischen Koordinatenebenen (z.B. xy) oder zylindrische Ebenen (z.B. radial-tangential), je nach Wahl des Ergebnis Koordinatensystems. Die nachfolgende Abbildung zeigt anhand des oben definierten Quadersystems graphisch das Bxz-Feld als Funktion der Pfadposition. Deformationsparameter ist hier 0.4. Die Werte können in allen Fällen sowohl als Listing als auch als Diagramm ausgegeben werden.

Tutorium 3.1

Lernen Sie hier die neuen Features von Version 3.1 kennen und handhaben. Dies betrifft im Detail drei neuen Arten von zweipoligen Sensormagneten mit Vertiefungen und Rändern.

Tutorium 3.2

Tutorium 3.3